In this month’s blog, we explore some of the statistical results from multivariate Gaussian distributions.  Typically, many of these results were developed in support of particular problems in science and engineering, but they stand on their own in that the results flow from the logic of statistical thinking that can be cleanly separated from the application that birthed them. 

The Monte Carlo method, which was the subject in a previous run of blogs (Monte Carlo Integration, Part 1 to Part 5), will be used here as an additional check on the techniques developed, but there will be no emphasis on the mechanics of these techniques.

For a typical, motivating example, consider the expectation value presented in Section 1.2 of Brezin’s text Introduction to Statistical Field Theory, which asks the reader to compute 

\[ E[x^4 y^2] = \frac{1}{N} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x^4 y^2 e^{-(x^2 + xy + 2 y^2)} \; , \]

where the normalization constant $N$ is given by

\[ N = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2 + xy + 2 y^2)} \; . \]

Examples like these arise in any discipline where the model describing a system depends on several (perhaps a huge number of) parameters that manifest themselves as inter-correlated variables that we can measure.  The cross-correlation between the variables $x$ and $y$ is displayed by the $xy$ term in the exponential.

The first task in determining the expectation value is to evaluate the normalization constant.  The general method for solving this task will be the focus of this installment. 

The method for integrating Gaussian integrals in one dimension is well known (see, e.g., here) but the approach for multivariate distributions is not as common.  The first point is to look at the quadratic form in the argument of the exponential as being built as the inner product between an array presenting the variables $x$ and $y$ and some matrix $A$.  In the present case this is done by recognizing

\[ x^2 + xy + 2 y^2 = \left[ \begin{array}{cc} x & y \end{array} \right] \left[ \begin{array}{cc} 1 & 1/2 \\ 1/2 & 2 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right]  \; . \]

Looking ahead to higher dimensional cases, we can see that this expression can be written more generally and compactly as $r^T A r \equiv r_i A_{ij} r_j$, where $r$ is a column array presenting the independent variable of the distribution (now imagined to be $n$ in number) and $A$ is a real $n \times n$ matrix; the superscript $T$ indicates that the transpose of the original array is being used. 

With this new notation, any $n$-dimensional Gaussian distribution can now be written as

\[ e^{-(r^T A r)}  \; . \]

Since this expression is symmetric in $r$, $A$ can be taken to be symmetric without loss of generality.  This observation guarantees that $A$ can be diagonalized by an orthogonal matrix $M$ such that $M^T A M = D$, $M^T M = M M^T = 1$, and $D$ is a diagonal matrix.  This, in turn, means that the quadratic form can be rewritten as

\[ r^T A r = r^T (M M^T) A (M M^T) r = \\ (r^T M) (M^T A M) (M r) = (r^T M) D (M^T r) \; . \]

The next step is to define a new set of variables defined by $s = M^T r$, which then decouples the multivariate distribution into a product of $D$ independent one-dimensional Gaussians:

\[ e^{ – (r^T A r) } = e^{ – (s^T D s) } = \prod_{i=1}^{n} e^{-d_i s_i^2} \; , \]

where the $\{d_i\}$ are the individual, on-diagonal elements of $D$ and the $\{s_i\}$.  For the integral to exist (i.e., converge), we need one additional stipulation: that all of the $d_i > 0$.  Said differently, we require that $A$ have positive eigenvalues (i.e., be positive definite).

The final step is to recognize that the measure of the integral changes in a convenient way when we make the substitution $r = M^T s$, since

\[ d^n r = det(M^T) d^n s = d^n s  \; , \]

where we’ve exploited the fact that, since $M$ is orthogonal, its determinant is 1.

Putting all of these pieces together we now have

\[ \int_{R^n} d^n e^{-(r^T A r} = \int_{R^n} d^n s \prod_{i=1}^n e^{-d_i s_i^2} = \prod_{i=1}^{n} \int_{-\infty}^\infty ds_i e^{-d_i s_i^2} \; .\]

Since the right-hand side is a product of independent Gaussian integrals, it simplifies to

\[\prod_{i=1}^{n} \int_{-\infty}^\infty ds_i e^{-d_i s_i^2} = \prod_{i=1}^{n} \sqrt{\frac{\pi}{d_i}} = \frac{\pi^{n/2}}{\sqrt{d_1 \cdots d_n}} \; . \]

The denominator of the last expression is the determinant of the $D$, which is also the determinant of $A$.  So, the final formula is

\[ \int_{R^n} d^n r e^{-(r^T A r)} = \frac{\pi^{n/2}}{\sqrt{det(A)}} \; .\]

Returning to the original example, the formula tells us that, since $det(A) = 7/4$, then the normalization constant $N = 2\pi/\sqrt(7) \approx 2.37482$.  We can confirm this using brute force Monte Carlo by uniformly sampling across the ranges $x \in [-6,6]$ and $y \in [-12,12]$.  The limits of these ranges were selected by going out roughly to 6 times the respective eigenvalue ($d_x = 0.79$, $d_y = 2.21$), but the estimated integral is insensitive to fine details as long as the computational domain is sufficiently large.  That said, there is an art to picking the computational domain, and sophisticated pieces of software are designed to adjust to the integrand.  Implementing the brute force Monte Carlo in python gave an estimate of $N = 2.37661$ for 10 million trials, an error of less than $0.1\%$.

As a last sample, suppose we provide a bigger matrix given by:

\[ A = \left[ \begin{array}{cccc} 3 & 1 & 5 & 3\\ 1 & 5 & 2 & 0\\ 5 &  2 & 10 & 3 \\ 3 & 0 & 3 & 14 \end{array} \right] \; .\]

The Gaussian integral is

\[ N = \int_{R^n} d^n r \,  e^{-(3w^2 + 2wx + 10wy + 6w^2 + 5x^2 + 4xy + 10y^2 + 6yz + 14z^2)} \; .\]

The eigenvalues of $A$ are: $\{17.63,0.26,9.85,4.26\}$.  Application of the formula gives $N = 0.70497$ compared with a brute force Monte Carlo estimate of $0.71061$.

With this operation well in hand, next month’s post will focus on calculating various moments of these distributions.

One of the persistent mysteries surrounding that art form that is called the mystery is exactly how to write a good one. Of course, there’s no denying that a command of the English language is essential.  So too is the ability to create such engaging characters that we want don’t want the mystery to end.  Indeed, the masters, such as Arthur Conan Doyle, G.K. Chesterton, Rex Stout, and Agatha Christie created such enduring characters that we enjoy visiting them again and again regardless of the crime underfoot.  And having a victim, either totally sympathetic or entirely loathsome, is important so that we can either enjoy righteous justice being meted out or secretly delight in someone getting what’s coming to him.  But foremost is the requirement, agreed to by tacit contract by the writer with the reader, that the detective’s solution be a satisfying explanation with surprises and ‘aha’ moments that nonetheless ties up all the loose ends.  As Chesterton puts it, the writer should provide a simple explanation of something that only appears complex; an explanation that doesn’t, itself, need an explanation.

There are several, classic ways that authors employ to add complexity to a mystery, to obscure what’s going on.  These include the red herring, in which an event or a set of clues lead nowhere and only serve as dust to cover the real trail.  Another classic approach is to provide so many extraneous details, typically by indulging in sumptuous descriptions of surroundings or detailed appearance and behaviors of the characters, that a vital clue is lost amid noise.  And, of course, there are accusations of authors who withhold vital clues and omit important details as is hilariously summarized in the final act of the movie Murder by Death. 

Omitting vital clues or important information is commonly considered unfair; a bad show which is against the rules of the implicit contract discussed above.  And yet, there is a way to omit something from a mystery while still playing fair with the reader.  This fair-play omission occurs when the writer leaves out the second of the Three Acts of the Mind thereby leaving out a judgement or predication of the facts already revealed, which any reader with common sense can make for himself but usually doesn’t.

For those unfamiliar with what philosophers mean by the three acts of the mind, a terse summary must suffice. The first act of the mind shows that mental faculty that allows a thing to grasp what is being observed.  For example, it is the ability we all possess to look a room and distinguish a chair from the pistol resting on the seat.  In the second act of the mind, a predication about some object observed in the first act is made such as the pistol is smoking.  The third act of the mind ties the various observations and their corresponding predications together with connective reasoning to conclude something like: since the pistol is still smoking and the cause of death is a bullet wound, the murder must have committed the crime only a short time before.

Omitting the second act of the mind doesn’t violate the contract since it neither steals a simple clue from the reader’s notice nor does it hide a clue in plain sight by requiring the reader to have narrow, specialized knowledge to understand it.  Rather, the writer shares information freely but doesn’t spoon feed the proper interpretation, relying, instead on the reader to provide it for himself.

An excellent example of how to omit the second act of the mind and thereby write an engaging mystery is Edgar Allen Poe’s Murders in the Rue Morgue.

This mystery, told by an unnamed narrator, centers on the horrific deaths of Madame L’Espanaye and her daughter Mademoiselle Camille L’Espanaye.  Both victims were “frightfully mutilated” with the mother being essentially decapitated by murderer using nothing more than an ordinary straight razor while the daughter’s battered and strangled corpse was shoved, head-down, up the chimney so far that the body “could not be got down until four or five of the party united their strength.”

Poe makes the mystery even more interesting by proving scores of witnesses who heard the screams of the women as the crime was unfolding.  A subset of these followed a gendarme into the house after the latter had forced entry and arrived on the scene, an upper-floor bedroom, in time to find the daughter’s corpse still warm.  The door from the hall into the bedroom was locked from the inside, the room itself was in shambles with the furnishings thrown about, and all its window were closed and locked.  Each of the witnesses who ascended the house during the murder testified to hearing two voices coming from above in “angry contention.”  The first voice was universally agreed to be the gruff voice of a French-speaking male.  The second voice, variously described as shrill or harsh, defied classification of the witnesses.  A French man thought the voice to be speaking Italian; an English man thought it to be German; a Spaniard thought it English; and so on.

Having laid out the facts, Poe then allows the reader some space before having his detective, C. Auguste Dupin, fill in the gaps.  Dupin provides the judgement (i.e., predication) of the facts that serve as the connective tissue between the simple apprehension of the facts (e.g., two voices in angry contention) and the solution of the crime.

Several of the interpretations that Dupin provides us become clear after their revelation but none so arresting as his insight into the inability of none witness to agree on the nationality of the shrill or harsh voice.  Poe puts in marvelously in this exchange between the Dupin and the narrator:

 
From this “peculiarity” in the testimony, Dupin supports the conclusion, arrived at deductively through the exercise of the third act of the mind, that the murderer was an orangutan.

This technique is not limited to Poe alone.  Consider the notable example found in Some Buried Caesar by Rex Stout.  The reader is given all the necessary facts about a bull accused on goring a man to death.  Indeed, the reader is just about spoon fed them just after the murder in a manner as plain as they would be presented in the final explanation.  Nonetheless, the solution remains surprising for many of us precisely because we don’t provide the correct predication.

While it is likely that host of authors use this technique, whether knowingly or instinctively, it is curious that the explicit connection what makes a satisfying solution to a mystery and the omission of the second act of the mind to ‘hide’ the solution in plain sight seems never to have been made.  And that is an omission we hope to correct.

As discussed in other posts, humor is a delicate thing even for rational (at least sometimes) human beings let alone for a machine intelligence the grasp. Case in point, a little joke that sneakily crept up on me all I was in a pub on a beach holiday.  It was the kind of joke that at first you likely don’t get and then the light bulb goes on after a few seconds and then the subtly of the humor hits you, much like that ‘ah-ha’ moment when you finally got the Pythagorean theorem or riding a bike or some other experiential thing.

The name of the place is Shenanigans.

Given that it is an Irish Pub, it’s hardly a surprise that the dining area would stimulate its public with various pieces of trivia and witticisms. Some of these witticisms extended beyond the usual humorous ones one would expect in a conventional bar setting and bordered on wisdom.  One in particular opened vistas of thought about language, meaning, ambiguity, and humor.The witticism in question, which really caught my attention, asked the following question:

The obvious answer, of course, depends on an equivocation in the verb to dry.In English, the action of drying can be interpreted as two distinct and opposite sequence of events. In the first, we have the passion – that is to say, the passive event – of an object as it dries out.  In this case, the object loses any water or other such liquid that it has been carrying or holding.  An excellent example of this being the ground drying after the sun has come out after a rainfall.  The object is simply bystander as it is subjected to the drying action performed by an external entity.  In the second, we have the action – that is to say, the active performance – of the entity that performs the drying action.  In the wet ground example mentioned earlier, the sun would perform the drying.  In older language that, sadly, has fallen out of favor, the sun is the drier and the ground the ‘driee’.    

Getting back to the witticism, the humor, obviously turns on the fact that the verb ‘dry’ is ambiguous in the present tense.  Consider the two sentences:

and

The first three words of each are identical with the same subject and verb.  The only clue that the first is the passive sense and the second the active one is the inclusion of the prepositional phrase ‘in the sun’.

At first glance, one might think that indicator is sufficient and a bit of parsing here and a bit of coding with a lookup table there and one has taught a machine to tell the difference.  Then one nips out to the pint and while drinking a pint of Guinness one realizes that the next sentence can be said with proper meaning and with equal probability of being either passive or active.

What’s a machine to do, you may ask?  Well… if it is to pass the Turing test it might randomly make an assumption and move forward or ask for clarification.  If the machine were being really ‘clever’ it might do both.

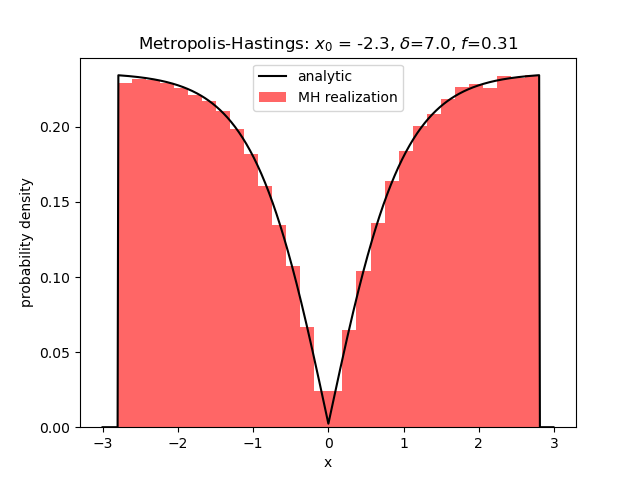
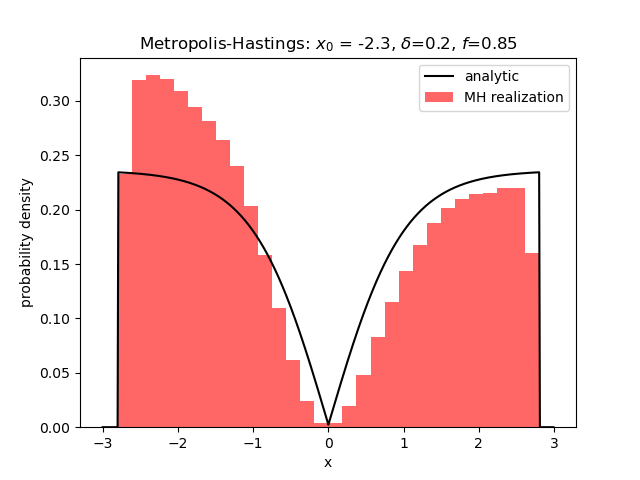
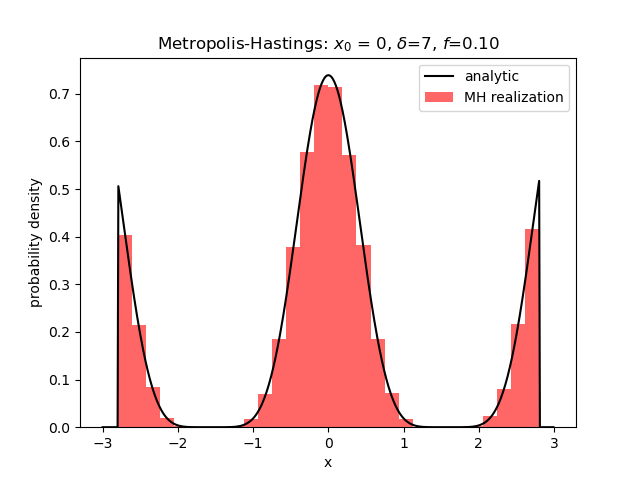
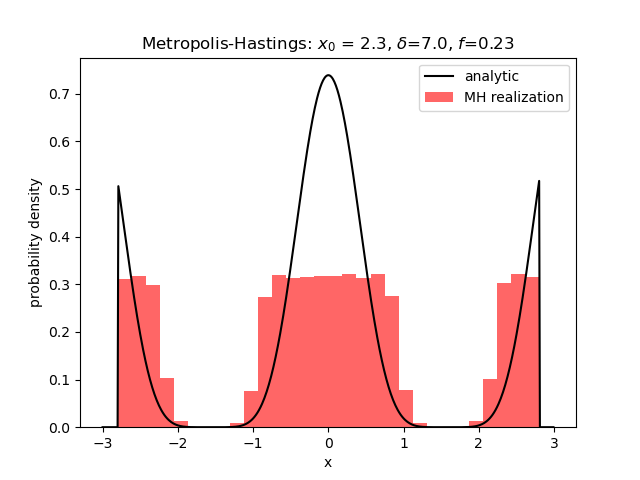
Our journey through various Monte Carlo techniques has been rich and rewarding but has been confined almost exclusively to one-dimensional sampling.  Even the case of the sunny/rainy-day multi-state Markov Chain (prelude and main act) was merely a precursor to the setup and analysis of the Metropolis-Hastings algorithm that was then applied in one dimension.  This month, we step off the real number line and explore the plane to understand a bit of how multivariate sampling works and the meaning of covariance.

To start, let’s imagine that we are measuring the height and weight of some mythical animal, say the xandu of C.S. Friedman’s Coldfire Trilogy.  Further suppose that we’ve measured 5000 members of the population and recorded their height and weight.  The following figure shows the distribution of these two attributes plus the quantitative statistics of the mean and standard deviation of each.

While these statistics give us a good description of the distribution of the weight or the height of the xandu population that don’t say anything about the connection between these two attributes.  Generally, we would expect that the larger an animal is the heavier that animal will be, all others things being equal.  To better understand the relationship between these two population characteristics, we first make a scatter plot of their weight arbitrarily displayed on the x-axis ($X$ will hereafter be a stand in symbol for weight) and their height along the y-axis ($Y$ for height).

It is obvious that the two attributes are strongly correlated.  To make that observation quantitative we first define the covariance matrix between the two series.  Let’s remind ourselves that the variance of a set of $N$ values of the random variable $X$, denoted by ${\mathbf X} = \left\{ x_1, x_2, \ldots , x_N\right\}$ defined as

\[ {\sigma_X}^2 = \frac{1}{N} \sum_{i=1}^N \left( x_i – {\bar x} \right)^2 \; , \]

where ${\bar x}$ is the mean value given by

\[ {\bar x} = \frac{1}{N} \sum_{i=1}^N x_i  \; . \]

We can express these relations more compactly by defining the common notation of an expectation value of $Q$ as

\[ E[Q] = \frac{1}{N} \sum_{i=1}^N q_i \; , \]

where $Q$ is some arbitrary set of $N$ values denoted as $q_i$.  With this definition, the variance becomes

\[ {\sigma_X}^2 = E \left[ (X – {\bar x})^2 \right] \; . \]

The covariance is then the amount the set $X$ moves with (or covaries) with the set $Y$ defined by

\[ Cov(X,Y) = E \left[ (X – {\bar x}) (Y – {\bar y} ) \right] \; .\]

Note that the usual variance is now expressed as

\[ {\sigma_X}^2 = Cov(X,X) = E \left[ (X – {\bar x}) (X – {\bar x}) \right] = E \left[ (X – {\bar x})^2 \right] \; , \]

which is the same as before.

There are four unique combinations: $Cov(X,X)$, $Cov(X,Y)$, $Cov(Y,X)$, and $Cov(Y,Y)$.  Because the covariance in symmetric in its arguments $Cov(Y,X) = Cov(X,Y)$.  For reasons that will become clearer below, it is convenient to display these four values in the covariance matrix

\[ {\mathcal P}_{XY} = \left[ \begin{array}{cc} Cov(X,X) & Cov(X,Y) \\ Cov(Y,X) & Cov(Y,Y) \end{array} \right] \; , \]

where it is understood that in real computations the off-diagonal terms are symmetric.

The computation of the covariance matrix for the data above is

\[ {\mathcal P}_{XY} = \left[ \begin{array}{cc} 19.22857412 & 17.51559386 \\ 17.51559386 & 39.54157185 \end{array} \right ] \; . \]

The large off-diagonal components, relative to the size of the on-diagonal components, reflects the strong correlation between weight and height of the xandu.  The actual correlation coefficient is available from the correlation ${\bar {\mathcal P}}_{XY}$ matrix defined as dividing the terms by the standard deviation of the arguments used

\[ {\bar {\mathcal P}}_{XY} = \left[ \begin{array}{cc} Cov(X,X)/{\sigma_X}^2 & Cov(X,Y)/\sigma_X \sigma_Y \\ Cov(Y,X)/\sigma_Y \sigma_X & Cov(Y,Y)/{\sigma_Y}^2 \end{array} \right] \; .\]

Substituting the values in yields

\[ {\bar {\mathcal P}}_{XY} = \left[ \begin{array}{cc} 1.00000 & 0.63577 \\ 0.63577 & 1.0000 \end{array} \right ] \; . \]

The value of 0.63577 shows that the weight and height are moderately correlated so that about 64% of the variation of the one explains the variation of the other.

With these results in hand, let’s return to why it is convenient to display the individual covariances in matrix form.  Doing so allows us to use the power of linear algebra to find the independent variations, $A$ and $B$, of the combined data set.  When the weight-height data are experimentally measured, the independent variations are found by diagonalizing the covariance matrix.  The resulting eigenvectors indicate the directions of independent variation (i.e., $A$ and $B$ will be expressed as some linear combination of $X$ and $Y$) and the eigenvalues are the corresponding variances ${\sigma_A}^2$ and ${\sigma_B}^2$.  The eigenvector/eigenvalue decomposition rarely yields results that are generally understandable as the units of the two variables different but, nonetheless, one can think of the resulting directions as arising from a rotation in the weight-height space.

Understanding is best achieved by using a contrived example where we start with known population parameters for $A$ and $B$ and ‘work forward’.  For this example, $\mu_A = 45$ and $\mu_B = 130$ with the corresponding standard deviations of $\sigma_A = 3$ and $\sigma_B = 7$, respectively.  These data are then constructed so that they differ from $X$ and $Y$ by a 30-degree rotation.  In other words, the matrix equation

\[ \left[ \begin{array}{c} X \\ Y \end{array} \right] = \left[ \begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array} \right] \left[ \begin{array}{c} A \\ B \end{array} \right] \; \]

relates the variations in $A$ and $B$ to the variation in $X$ and $Y$, where $\theta = 30^{\circ}$.  It also relates the mean values by

\[ \left[ \begin{array}{c} \mu_X \\ \mu_Y \end{array} \right] = \left[ \begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array} \right] \left[ \begin{array}{c} \mu_A \\ \mu_B \end{array} \right] \; , \]

yielding values of $\mu_X = 103.97114317$ and $\mu_Y = 90.08330249$.  Note that these are exact values and that the means calculated earlier are estimates based on the sampling. 

The exact covariance can also be determined from

\[ {\mathcal P}_{XY} = M {\mathcal P}_{AB} M^{T} \; , \]

where the diagonal matrix ${\mathcal P}_{AB} = diag({\sigma_A}^2,{\sigma_B}^2)$ reflects the fact that $A$ and $B$ are independent random variables and where the ‘$T$’ superscript means the transpose.  The exact value is

\[ {\mathcal P}_{XY} = = \left[ \begin{array}{cc} 19.0 & 17.32050808 \\ 17.32050808 & 39.0 \end{array} \right] \; . \]

Again, note both the excellent agreement with what has been estimated from the sampling. 

These methods generalize to arbitrary dimension straightforwardly.

Finally, all of the sampling here was done using numpy, which conveniently has a multivariate sampling method.  The only draw back is that it requires knowledge of the exact means and covariances so the above method of mapping $A$ and $B$ to $X$ and $Y$ is necessary.  It is instructive to see how well the multivariate sampling matches the method used above in both scatter plot

and in the individual distributions for weight

and height

Last month’s posting introduced the Metropolis-Hastings (MH) method for generating a sample distribution from just about any functional form.  This method can in handy particularly for methods that are analytically intractable so that the inverse-transform method would be useless and for which the accept-reject method would be too inefficient. 

The Metropolis-Hastings algorithm, which is particular instance of the broader Markov Chain Monte Carlo (MCMC) methods, brings us the desired flexibility at the expense of being computationally more involved and expensive.  As a reminder, the algorithm works as follows:

• Setup
  • Select the distribution $f(x)$ from which a set random numbers are desired
  • Arbitrarily assign a value to a random realization $x_{start}$ of the desired distribution consistent with its range
  • Select a simple distribution $g(x|x_{cur})$, centered on the current value of the realization from which to draw candidate changes
• Execution
  • Draw a change from $g(x|x_{cur})$
  • Create a candidate new realization $x_{cand}$
  • Form the ratio $R_f = f(x_{cand})/f(x_{cur})$
  • Make a decision as the keeping or rejecting $x_{cand}$ as the new state to transition to according to the Metropolis-Hastings rule
    • If $R_f \geq 1$ then keep the change and let $x_{cur} = x_{cand}$
    • If $R_f < 1$ then draw a random number $q$ from the unit uniform distribution and make the transition if $q < R_f$

and the explicit promise of this month’s installment was the explanation as to why this set of rules actually works. 

Technically speaking, the algorithm, as written above, is strictly the Metropolis-Hastings algorithm for the case where the simple distribution $g(x|x_{cur})$ is symmetric; the modification for the case of non-symmetric distributions will emerge naturally in the course of justification for the rules.

The arguments presented here closely follow the excellent online presentation by ritvikmath:

To start, we relate our distribution $f(x)$ to the corresponding probability by

\[ p(x) = \frac{f(x)}{N_C} \; , \]

where $N_C$ is the normalization constant that is usually impossible to calculate analytically either because the functional form of $f(x)$ possess no analytic anti-derivative or the distribution is defined in high dimensions or both.

The MH algorithm pairs $p(x)$ with a known probability distribution $g(x)$ but in a way such that the algorithm ‘learns’ where to concentrate its effort by having $g(x)$ follow the current state around (in contrast to the accept-reject method where $g(x)$ is stationary).  At each step, the transition from the current state $a$ to the proposed or candidate next state $b$ happens according to the transition probability

\[ T(a \rightarrow b) = g(b|a) A(a \rightarrow b) \; , \]

where $g(b|a)$ is conditional draw from $g(x)$ centered on state $a$ (i.e., $g$ follows the current state around) and the transition probability $A(a \rightarrow b)$ is the MH decision step.  The right-hand-side of the transition probability directly maps $g(b|a)$ and $A(a \rightarrow b)$ to the first two and the last two sub-bullets of the execution step above, respectively. 

To derive the MH decision step correctly describes $A(a \rightarrow b)$, we impose detailed balance,

\[ p(a) T(a \rightarrow b) = p(b) T(b \rightarrow a) \; \]

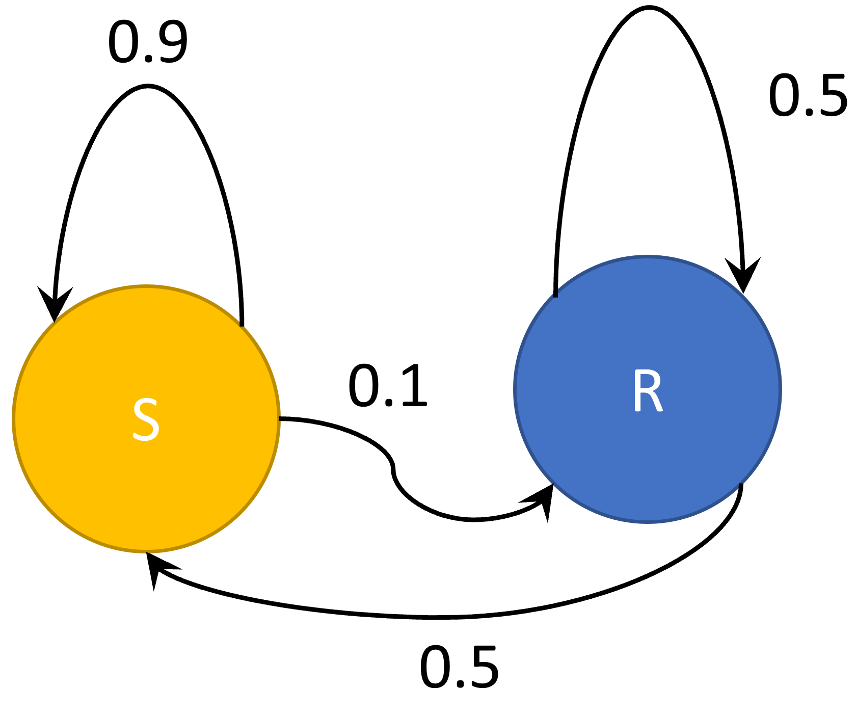
guaranteeing that the MCMC will eventually result in a stationary distribution.  That detailed balance give stationary distributions of the Markov chain is most easily seen by summing both sides over $a$ to arrive at a matrix analog of the stationary requirement ${\bar S}^* = M {\bar S}^*$ used in the Sunny Day Markov chain post.

The next step involve a straightforward plugging-in of earlier relations to yield

\[ \frac{f(a)}{N_C} g(b|a) A(a \rightarrow b) = \frac{f(b)}{N_C} g(a|b) A(b \rightarrow a) \; . \]

 Collecting all of the $A$’s over on one side gives

\[ \frac{A(a \rightarrow b)}{A(b \rightarrow a)} = \frac{f(b)}{f(a)} \frac{g(a|b)}{g(b|a)} \; . \]

Next define, for convenience, the two ratios

\[ R_f = \frac{f(b)}{f(a)} \; \]

and

\[ R_g = \frac{ g(a|b) }{ g(b|a) }  \; . \]

Note that $R_f$ is the ratio defined earlier and that $R_g$ is exactly 1 when the $g(x)$ is a symmetric distribution.

Now, we analyze two separate cases to make sure that the transitions $A(a \rightarrow b)$ and $A(b \rightarrow a)$ can actually satisfy detailed-balance. 

First, if $R_f R_g  < 1$ then detailed balance will hold if we assign $A(a \rightarrow b) = R_f R_g$ and $A(b \rightarrow a) = 1$.  These conditions mean that we can interpret $A(a \rightarrow b)$ as a probability for making the transition and we can then draw a number $q$ from a uniform distribution to see if we beat the odds $q \leq R_f R_g$, in which case we transition to the state $b$.

Second, if $R_f R_g \geq 1$ then detailed balance will hold is we assign $A(a \rightarrow b) = 1$ and $A(b \rightarrow a) = R_f R_g$.  These conditions mean that we can interpret $A(a \rightarrow b)$ is being a demand, with 100% certainty, that we should make the change.

These two cases, which comprise the MH decision rule, are often summarized as

\[ A(a \rightarrow b) = Min(1,R_f R_g) \; \]

or, in the case when $g(x)$ is symmetric

\[ A(a \rightarrow b) = Min\left(1,\frac{f(b)}{f(a)}\right) \; , \]

which is the form used in the algorithm listing above.

The last two columns explored the notion for transition probabilities, which are conditional probabilities that express the probability of a new state being realized some system given the current state that the system finds itself in.  The candidate case that was examined involved the transition probabilities of between weather conditions (sunny-to-rainy, sunny-to-sunny, etc.).  That problem yielded answers via two routes: 1) stationary analysis using matrix methods and 2) Markov Chain Monte Carlo (MCMC). 

The analysis of the weather problem left one large question looming.  Why anyone would ever use the MCMC algorithm when the matrix method was both computationally less burdensome and also gave exact results compared to the estimated values that naturally arise in an Monte Carlo method.

There are many applications but the most straightforward one is the Metropolis-Hasting algorithm for producing pseudorandom numbers from an arbitrary distribution.  In an earlier post, we presented an algorithm for producing pseudorandom numbers within a limited class of distributions using the Inverse Transform Method.  While extremely economical the Inverse Transform Method depends on the finding invertible relationship between a uniformly sampled pseudorandom number $y$ and the variable $x$ that we want distributed according to some desired distribution.

The textbook example of the Inverse Transform Method is the exponential distribution.  The set of pseudorandom numbers given by

\[  x = -\ln (1-y) \; , \]

where $y$ is uniformly distributed on the interval $[0,1]$, is guaranteed to be distributed exponentially. 

If no such relationship can be found, the Inverse Transform Method fails to be useful. 

The Metropolis-Hastings method is capable to overcoming this hurdle at the expense of being computationally much more expensive.  The algorithm works as follows:

• Setup
  • Select the distribution $f(x)$ from which a set random numbers are desired
  • Arbitrarily assign a value to a random realization $x_{start}$ of the desired distribution consistent with its range
  • Select a simple distribution $g(x|x_{cur})$, centered on the current value of the realization from which to draw candidate changes
• Execution
  • Draw a change from $g(x|x_{cur})$
  • Create a candidate new realization $x_{cand}$
  • Form the ratio $R = f(x_{cand})/f(x_{cur})$
  • Make a decision as the keeping or rejecting $x_{cand}$ as the new state to transition to according to the Metropolis-Hastings rule
    • If $R \geq 1$ then keep the change and let $x_{cur} = x_{cand}$
    • If $R < 1$ then draw a random number $q$ from the unit uniform distribution and make the transition if $q < R$

The bulk of this algorithm is very straightforward and simple.  The only confusing part is the Metropolis-Hastings decision rule in the last step and why it requires the various pieces above to work.  The next post will be dedicated to a detailed discussion of that rule.  For now, we’ll just show the algorithm in action with various forms of $f(x)$ which are otherwise intractable.

The python code for implementing this algorithm is relatively simple.  Below is a snippet from the implementation that produced the numerical results that follow.  The key points to note are:

• the numpy unit uniform distribution ($U(0,1)$) random was used for both $g(x|x_{cur})$ and the Metropolis-Hastings decision rule
• N_trials is the number of times the decision loop was executed but is not the number of resulting accepted or kept random numbers, which is necessarily a smaller number
• delta is the parameter that governs the size of the candidate change (i.e., $g(x|x_{cur}) = U(x_{cur}-\delta,x_{cur}+\delta)$
• n_burn is the number of initial accepted changes to ignore or throw away (more on this next post)
• x_0 is the arbitrarily assigned starting realization value
• prob is a pointer to the function $f(x)$

In addition to these input parameters, the value $f = N_{kept}/N_{trials}$ was reported.  The rule of thumb for Metropolis-Hastings is to have a value $0.25 \leq f \leq 0.33$.

x_lim    = 2.8
N_trials = 1_000_000
delta    = 7.0
Ds       = (2*random(N_trials) - 1.0)*delta
Rs       = random(N_trials)
n_accept = 0
n_burn   = 1_000
x_0      = -2.0
x_cur    = x_0
prob     = pos_tanh
p_cur    = prob(x_cur,-x_lim,x_lim)
 
x = np.arange(-3,3,0.01)
z = np.array([prob(xval,-x_lim,x_lim) for xval in x])
 
kept = []
for d,r in zip(Ds,Rs):
    x_trial = x_cur + d
    p_trial = prob(x_trial,-x_lim,x_lim)
    w       = p_trial/p_cur
    if w >= 1 or w > r:
        x_cur = x_trial
        n_accept += 1
        if n_accept > n_burn:
            kept.append(x_cur)

Two arbitrary and difficult functions were used for testing the algorithm:  $f_1(x) = |tanh(x)|/N_1$ and $f_2(x) = \cos^6 (x)/N_2$.  $N_1$ and $N_2$ are normalization constants obtained by numerically integrating over the range $[-2.8,2.8]$, which was chosen for strictly aesthetic reasons (i.e., the resulting plots looked nice).

The two parameters that had the most impact of the performance of the algorithm were the values of delta and x_0. The metric chosen for the ‘goodness’ of the algorithm is simply a visual inspection of how well the resulting distributions matched the normalized probability density functions $f_1(x)$ and $f_2(x)$.

Case 1 – $f_1(x) = |tanh(x)|/N_1$

This distribution was chosen since it has a sharp cusp in the center and two fairly flat and broad wings.  The best results came from a starting point $x_0 = -2.3$ over in the left wing (the right wing also worked equally well) and a fairly large value of $\delta=7.0$ was chosen such that $f \approx 1/3$.  The agreement is quite good.

A smaller value of $\delta$ lead to more samples being collected ($f=0.85$) but the realizations couldn’t ‘shake off the memory’ that they started over in the left wing and the results were not very good, although the two-wing structure can still be seen.

Starting off with $x_0 = 0$ resulted in a realization of random numbers that looks far more like the uniform distribution than the distribution we were hunting.

This result persists with smaller values of $\delta$.

Case 2 – $f_2(x) = \cos^6(x)/N_2$

In this case, the distribution has a large central hump or mode and two truncated wings.   The best results came from a starting value of $x_0$ at or near zero and a large value of $\delta$.

Lowering the value of $\delta$ leads to the algorithm being trapped in the central peak with no way to cross into the wings.

Finally, starting in the wings with a large value of $\delta$ leads to a realization that looks like it has the general idea as to the shape of the distribution but without the ability to capture the fine detail.

This behavior persists even when the number of trials is increased by a factor of 10 and no immediately satisfactory explanation exists.

In the last post, we demonstrated that not all conditional probabilities are conceptually equal even if they are linguistically equal.  The specific case discussed at the end – the sunny day case – doesn’t fit the usual mold.  To better understand why it doesn’t fit let’s looks back at the textbook case.

Ordinarily, we calculate a conditional probability by fixing one of the variables from a joint probability distribution and renormalizing so that ‘the probability of $B$ given $A$’, denoted by $P(B|A)$ obeys all the axioms of probability theory.  For simplicity, the joint probability distribution in the previous analysis was presented as a table (e.g. color and life of a bulb or snack preference based on sex) but any mathematically multi-variate function capable of being normalized serves.

But the sunny day case is different.  In that case, we define transition probabilities that express what the chance that the weather tomorrow will be like given the weather today, where there were only two possible outcomes: ‘Sunny’ (denoted as $S$) and ‘Rainy’ (denoted as $R$).  The conditional probabilities were:

\[ P(S|S) = 0.9 \; \]

and

\[ P(R|S) = 0.1 \; , \]

for the weather tomorrow based on today’s weather being sunny.  Likewise,

\[ P(S|R) = 0.5 = P(R|R) \; ,\]

 given that today is rainy.

It isn’t all clear how many actual variables we have in the joint probability distribution.  Is it 2, one for today and one for tomorrow?  Clearly that’s wrong since in any given span of days, say the month of September, taken in isolation, there are 28 days that serve as both a today and a tomorrow and 1 day each that is either a tomorrow or a today but not both.  As we’ll see below, in a real sense there are an infinite number of variables in the joint distribution since there are limitless todays and tomorrows (ignoring the obvious conflict with modern cosmology).

The question left hanging was just how could we determine the probability that, given an $N$-day long span of time, the weather on any given day was sunny.

This type of problem is called a Markov chain problem defined as the type of problem where the transition probabilities only depend on the current state and not something further back.  This type of system is said to have no memory.

There are two equally general methods for computing the long term probability of any given day being sunny or rainy but they differ in convenience and scope.  The first is the analytic method.

In the analytic method, we express the state of the system as a vector ${\bar S}$ with two components stating the probability of getting a sunny or rainy day.  The transition rules express themselves nicely in matrix form according to

\[ {\bar S}_{tomorrow} = M {\bar S}_{today} \; ,\]

which has the explicit form

\[ \left[ \begin{array}{c} S \\ R \end{array} \right]_{tomorrow} = \left[ \begin{array}{cc} 0.9 & 0.5 \\ 0.1 & 0.5 \end{array} \right] \left[ \begin{array}{c} S \\ R \end{array} \right]_{today} \; . \]

The explicit form of $M$ can be checked against an initial, known state of either ${\bar S}^{(0)} = [1,0]^{T}$ for sunny or ${\bar S}^{(0)} = [0,1]^{T}$ for rainy.

The matrix $M$ links the weather state today to that of tomorrow and we can think of it as an adjacency matrix for the following graph

with the interpretation that the edge weightings are the conditional transition probabilities.

Now lets place an index on any given day just to keep track.  The state of the n^th day is related to the initial state by

\[ {\bar S}^{(n)} = M {\bar S}^{(n-1)} = M^n {\bar S}^{0} \; .\]

Since we would like to know the probability of picking a sunny day from a collection of days, we are looking for a steady state solution, one which is immune to random fluctuations associated with a string of good or bad luck.  This special state ${\bar S}^{*}$ must correspond to $n \rightarrow \infty$ and so it must remain unchanged by successive applications of $M$ (otherwise it doesn’t represent a steady state).  Mathematically, this condition can be expressed as

\[ {\bar S}^{*} = M {\bar S}^{*}  \; , \]

or, in words, ${\bar S}^{*}$ is an eigenvector of $M$. Computing the eigenvectors of $M$ is easy with numpy and the results are

\[ {\bar S}^{*}_{\lambda_1} = [0.98058068, 0.19611614]^{T} \; \]

and

\[ {\bar S}^{*}_{\lambda_2} = [-0.70710678, 0.70710678]^{T} \; \]

for $\lambda_1 = 1$ and $\lambda_2 = 0.4$.  We reject the vector corresponding to $\lambda_2$ because it has negative entries which can’t be interpreted as probabilities.  All that is left is to scale ${\bar S}^{*}_{\lambda_1}$ so that the sum of the entries is 1.  Doing so gives,

\[ {\bar S}^{*} = [0.8333{\bar 3},0.16666{\bar 6}]^{T} \; ,\]

where the subscript has been dropped as it serves no purpose.

While mathematically correct, one might feel queasy about $\lim_{n\rightarrow \infty} M^n$ converging to something meaningful.   But a few numerical results will help support this argument. Consider the following 3 powers of $M$

\[ M^2 = \left[ \begin{array}{cc} 0.86 & 0.70 \\ 0.14 & 0.3 \end{array} \right] \; ,\]

\[ M^{10} = \left[ \begin{array}{cc} 0.83335081 & 0.83324595 \\ 0.16664919 & 0.16675405 \end{array} \right] \; ,\]

and

\[ M^{20} = \left[ \begin{array}{cc} 0.83333334 & 0.83333332 \\ 0.16666666 & 0.16666668 \end{array} \right] \; .\]

Clearly, repeated powers are causing the matrix to converge and the elements that obtain in the limit are the very probabilities calculated above and, by the time $n=20$ we have essentially reached steady state.

The second method is numerical simulation where we ‘propagate’ an initial state forward in time according to the following rules:

1. draw a uniform random number in the range $P \in [0,1]$ (standard range)
2. if the current state is $S$ then
   1. set the new state to $S$ if $P \leq 0.9$
   1. else set the new state to $R$
3. if the current state is $R$ then
   1. set the new state to $S$ is $P \leq 0.5$
   1. else set the new state to $R$
4. Record the new state and repeat

An alternative way of writing the same thing reads

1. draw a uniform random number in the range $P \in [0,1]$ (standard range)
2. if the current state is $S$ then
   1. set the new state to $R$ if $P \leq 0.1$
   1. else set the new state to $S$
3. if the current state is $R$ then
   1. set the new state to $R$ is $P \leq 0.5$
   1. else set the new state to $R$
4. Record the new state and repeat

Of course, hybridizations of these rule sets where block 2 in the first set if matched with block 3 in the second and vice versa also give the same results.  It is a matter of taste.

In any event, these rules are easy to implement in python and the following plot shows the fraction of $S$’s as a function of the number of times the rule has been implemented

The dotted line shows the value for the probability of a sunny day obtained from the first method and  clearly the simulations shows that it converges to that value.  This sunny/rainy day simulation is an example of Markov Chain Monte Carlo, which will be the subject of upcoming blogs.

It is an interesting aspect of human language that exactly the same wording can mean exactly different things, with each variation hiding subtle nuances of meaning and context.  This well-established principle makes human language expressive and evocative but also tends to obscure the channels of communication where precise communication is required.  Case in point, the use of conditional probability.

Consider the following two ‘cause-and-effect’ scenarios.  In the first, we survey two groups, each with 140 individuals, who are afflicted with similar diseases: a mild case of the flu and the common cold.  For our research purposes, we focus on only two of the set of symptoms common to both ailments and ask whether an individual complains more about having a sore throat or body aches.

Given the current statistics, medical community estimates that for a case of mild flu, patients rank the sore throat as more bothersome than body aches 57.14% of the time and body aches more bothersome 42.86% of the time.  The corresponding rankings for the common cold are 63.33% and 36.67% of the time for sore throat and body aches, respectively.

These rankings represent the conditional probabilities stating that if we know that an individual has a given disease then we should, within some statistical fluctuation, be able to say the probability that that individual will rank a sore throat ahead of body aches.  Alternatively, given a sample of patient, each known to have either a mild flu or the common cold, we should be able to say what proportion of them will rank which symptom as being worse.

To be concrete, consider that we have $N_f = 140$ people suffering with the flu and $N_c = 150$ with the common cold.  The proportions of these individuals that are predicted to rank the sore throat more would be given by the product of the conditional probability by the total size of the group.  Mathematically, the number of flu patients $N_{sf}$ ranking the sore throat as the primary problem is

\[ N_{sf} = P(s|f) N_f = 0.5714 \cdot N_f = 80 \; , \]

while the number of cold patients $N_{sc}$ agreeing that the sore throat is worse is

\[ N_{sc} = P(s|c) N_c = 0.4286 \cdot 140 = 60 \; . \]

In the same way, the number of flu and cold patients ranking body aches first can be obtained.  The results summarize nicely in the usual joint probability table we know from statistics

This is one way, and probably the most familiar way, of defining what is meant by conditional probability.  Other textbook examples involve surveying a population for attributes like the Christmas tree light example with the joint probability table

In order to follow what comes next, it is important to note that having the conditional probabilities is equivalent to having the table or vice versa.  Having the complete information represented in one form allows the unambiguous construction of the other.

Interestingly, there seems to be a case in which the term ‘conditional probability’ is used such that, as far as I can tell, the values can’t be meaningfully cast into table form like the above.  This case occurs when the use of the phrase ‘conditional probability’ is meant as a transition probability.  A textbook example of this is given in terms of the weather in the Wikipedia article on Examples of Markov Chains.

In this example, the conditional probabilities represent the chance that the weather tomorrow will be like the weather today.  For the sake of simplicity, the only two possible weather outcomes are ‘Sunny’ and ‘Rainy’.  The chance that it will be Sunny tomorrow given that it is Sunny today is 0.9.  Likewise, the chance that it will be Rainy tomorrow given that it is Sunny today is 0.1.  These facts are summarized in the conditional probabilities

\[ P(S|S) = 0.9 \; \]

and

\[ P(R|S) = 0.1 \; . \]

In a similar fashion, the conditional probabilities for a Sunny or Rainy tomorrow given that it is Rainy today are fifty-fifty

\[ P(S|R) = 0.5 = P(R|R) \; .\]

These conditional probabilities look, at first glance, to be on the same footing as the earlier ones.  The wording is the same; the notation is the same.  However, the interpretation is quite different.  The difference seems to lie in the fact that in the first case, the notion of having the flu or a cold and ranking which was worse, a sore throat or body aches, are underlying attributes of the sick individual.  In the second case, sunny or rainy weather is an attribute of the environment plain enough but the fact that there are an unlimited number of possibilities (e.g. SSRS for a four day sequence of weather with S = Sunny and R = Rainy) precludes making the usual table.

Mathematically, the heart of the difficult lies in the usual definition of a conditional probability in terms of sets.  For two possible outcomes $A$ and $B$ in a universe of possibilities the conditional probability that $B$ will occur given $A$ is

\[ P(B|A) = \frac{P\left( B \bigcap A \right)}{P(A)} \; , \]

where $P\left(B \bigcap A\right)$ is the probability of $A$ and $B$ occurring together (hence appearing in the joint probability distribution).  For example, in the Christmas tree light example above, the probability that a bulb chosen at random is both yellow and has a long life is

\[ P\left(long \bigcap yellow \right) = 0.0375 \; ,\]

while the probability of choosing a yellow bulb to begin with is

\[ P(yellow) = 0.15 \; . \]

The conditional probability given that the bulb is yellow that it also has a long life is

\[ P(long|yellow) = \frac{ P\left( long \bigcap yellow \right)}{P(yellow)} = \frac{0.0375}{0.15} =  0.25 \; . \]

So, we can move easily between conditional probabilities and joint probability distributions in this case.

In the case of the transition probabilities between weather, it isn’t clear how to encode the event $S$ as sunny today versus $S$ as sunny tomorrow.  The concepts of today and tomorrow are relative and constantly shifting during the passage of time.

One’s first reaction to that might be to not care.  But then how does one answer the simple question as to the proportion of days that are sunny?  This will be the topic of next month’s column.

This month we examine some of the specialized algorithms and packages that have been developed over several decades to perform importance sampling in a variety of scenarios.  Before digging to the specifics, it is worth setting the stage as to why importance sampling is such a key part of many problems.

A number of fields deal with high dimensional integrals.  Most likely, the original scenarios involving such integrals came about in connection to many-particle physics.  They arise in computing so-called loop corrections to quantum field theories which have the form

\[ I = \int d^3 k_1 d^3 k_2 \ldots d^3 k_n f({\vec k}_1, {\vec k}_2, \ldots ,{\vec k})_n \; , \]

where the ${\vec k}_i$ are the spatial momenta for the $i^{th}$ particle involved.  Likewise, the classical statistical description of the motion of group of $N$ particles involves computing the partition function given by

\[ Z = \int d^3 q_{(1)} d^3 p^{(1)} \ldots d^3 q_{(N)} d^3 p_{(N)} f(q^{i}_{(1)},p_{j}^{(1)},\ldots, q^{i}_{(N)},p_{j}^{(N)} ) \; , \]

where the $q^{i}_{(J)}$ and $p_{i}^{(J)}$ are the generalized coordinates and momenta for the $J^{th}$ particle and $f$ describes the interaction. 

In more recent years, high dimensional integrals have found a place in modeling images (ray tracing,  path tracing, and production rendering) and in mathematical finance, to name only a few.

Clearly, any system with sufficiently high number of continuous degrees of freedom is apt to birth an integral that has more dimensions than what can be efficiently dealt with using the more traditional structure quadrature methods – hence the need for Monte Carlo.  What is not so obvious is that, generically, the integrands are likely to be tightly peaked in only a small fraction of the total volume – hence requiring importance sampling.

This later point is typically easier to understand with a simple example in which we estimate the percentage of the volume of unit width consume by a sphere of unit diameter inscribed in the box.  In one dimension, the box extends over the range $[-0.5,0.5]$ and the sphere, defined as all the points within a distance of $0.5$ from the origin, are coincident.  The 1-sphere has two points where it touches the edge and there are no corners outside and thus it consumes 100% of the volume of the inscribing box.  In two dimensions, the box extends of the range $[-0.5,0.5]$ along two axes and the 2-sphere has volume $V = \pi (0.5)^2$.  There are four points where the 2-sphere touches the edge of the box and there are four corners that lie outside.  The 2-sphere only consumes 78.5% of the volume of the box.  In three dimensions, the volume of the 3-sphere is $V = 4\pi/3 (0.5)^2$ leaving 8 corners to lie outside and only 52.8% of the volume consumed.  A compact generalized formula for the volume of sphere in $N_D$-dimensions is given by

\[ V_{N_D} = \frac{\pi^{N_D/2}}{\Gamma \left(\frac{N_D}{2} + 1 \right)} \; .\]

The following plot shows just how quickly the volume fraction plummets to zero as the number of dimensions increases. 

At $N_D=20$ the 20-sphere touches all $2^20$ faces of the box but only at one point thus failing to include the $2^20$ corners containing points with distances greater than $0.5$ from the origin leading to an amazingly small percentage (0.0000025%) of the total volume occupied.  So, even in a scenario where the integrand seems ‘spread out’ the important region of the function is strongly peaked.

It is against this backdrop that we find several multi-purpose Monte Carlo importance sampling algorithms. 

Perhaps the oldest and most revered algorithm is VEGAS authored by G. Peter LePage in 1978.  VEGAS, which has its roots in particle physics, works by first ‘feeling out’ the integrand, looking for regions where the integrand is large in magnitude.  The algorithm grids the space coarsely to begin with and samples the function to make a histogram.  It then refines the sampling along each coordinate direction but avoids the combinatoric issues associated with structured quadrature by assuming that the integrand is separable in the sense that

\[ f(x_1, x_2, \ldots) = f_1(x_1) f_2(x_2) \ldots \; . \]

Having identified those regions with this adaptive gridding, VEGAS then concentrates the subsequent Monte Carlo trials using importance sampling to produce an estimate of the integral with an approximately minimized variance.

Roughly two decades after the release of VEGAS, Thorsten Ohl proposed an improvement to VEGAS in his paper entitled Vegas Revisited: Adaptive Monte Carlo Integration Beyond Factorization, in which he addresses the assumption that the integrand is separable.  Ohl found that his algorithm VAMP “show[ed] a significantly better performance for many ill-behaved integrals than Vegas.”  It isn’t clear how widely accepted VAMP has become but clearly some of the improvements that VAMP sought to add to VEGAS have been included in the new version of called VEGAS+.  Lepage’s article Adaptive Multidimensional Integration: VEGAS Enhanced describes the improvements in VEGAS+ over classic VEGAS, including a new adaptive stratified sampling algorithm.  Lepage provides both a free software python package on GitHub and comprehensive documentation.  Stratified sampling is a complementary method to importance sampling where the Monte Carlo samples are preferentially placed in regions where the integrand changes rapidly rather than strictly in regions where its magnitude is large.  The classic algorithm in stratified sampling is MISER but discussing it is out of scope in this analysis of importance sampling.  Suffice to say that both VEGAS and MISER are sufficiently important that they the only Monte Carlo algorithms packaged in the GNU scientific library.

In the last installment, we touched on the first rudiments of importance sampling as a way of improving the Monte Carlo estimation of integrals.  The key relationship is that a Monte Carlo estimate of an integral $I$ is given

\[ I = \int_a^b \, dx \, f(x) \approx \frac{1}{N} \sum_i \frac{f(x)}{p(x)} \pm \frac{\sigma}{\sqrt{N}} \; , \]

where $p(x)$ is a known probability distribution and $N$ are the number of Monte Carlo trials (i.e. random samples).

The error in the estimate depends on two terms: the number of Monte Carlo trials $N$ and the sample standard deviation $\sigma$ pulled at random from $p(x)$.  Although the error in the estimation can be made as small as possible by increasing the number of trials, the convergence is rather slow.  The importance sampling strategy is to make each Monte Carlo trial count as much as possible by adapting $p(x)$ to the form of $f(x)$ such that the ratio of the two terms is a close as possible to being a constant.

The examples of how to implement this strategy from the last post were highly contrived to illustrate the method but are not representative of what is actually encountered in practice since the majority of integrands are complicated and often no able to even be represented in closed form.

In this post, we are going to extend this method a bit by considering examples where the ratio of $f(x)/p(x)$ is not a constant.

Our first example will be to estimate the integral

\[ I = \int_{0}^{10} \, dx \, e^{-x^2} \; . \]

Up to an overall scaling this integral is proportional to the error function defined as

\[ erf(z) = \frac{2}{\sqrt{\pi}} \int_0^z \, dx e^{-x^2} \; . \]

While the error function is special function that can’t be expressed as a finite number of elementary terms, it has been studied and cataloged and, like the trigonometric functions, can be thought of as being a known function with optimized ways of getting a numerical approximation.  Our original integral is then

\[ I = \frac{\sqrt{\pi}}{2} erf(10) \approx 0.886226925452758 \; , \]

which we take as the exact, “truth” value.

To start we are going to estimate this integral using two different probability distributions: the uniform distribution, to provide the naïve Monte Carlo baseline for comparison, and the exponential distribution $p(x) \propto \exp(-x)$.  While the exponential distribution doesn’t exactly match the integrand (i.e. $exp(-x^2)/exp(-x) \neq \textrm{constant}$), it falls off similarly

and will provide a useful experiment to set expectations of what the performance will be when $p(x)$ only approximately conforms to $f(x)$.  Using the exponential distribution will also provide another change to use the variable substitution method for generating probability distributions. 

To generate an exponential distribution, we assume $y$ random variable related to the random variable $x$ through an integral where the exponential distribution is the integrand

\[ y = \int_{0}{x} \, dt e^{-t} \; .\]

Since $y$ is the cumulative distribution function it sits on the range $[0,1]$ and when it is uniformly distributed $x$ will be exponentially distributed.  The only remaining step is to express $x$ in terms of $y$.  For the exponential distribution, this is easily done as the integral is elementary.  Carrying out that integration gives

\[ y = \left. – e^{-t} \right|_{0}^{x} = 1 – e^{-x} \; .\]

Solving for $x$ yields

\[ x = -\ln (1-y) \; .\]

This relation is very simple to implement in python and a $N=10,000$ set of uniform random numbers for $y$ results the following histogram for the distribution for $x$,

which has a mean of $s_x = 1.00913$ and a $\sigma_x = 0.98770$ compared to the exact result for both being $1$.

Of course, most programming languages have optimized forms of many distributions and python is no different so we could have used the built-in method for the exponential distribution.  Nonetheless, following the above approach is important.  Understanding this class of method in detail reveals when it can and cannot work and illustrates some of the difficulties encountered in generating pseudorandom numbers from arbitrary distributions.  It helps to explain why some distributions are ‘built-in’ (e.g. the exponential distribution) when others, say a distribution proportion to a fifth-order or higher order polynomial over a finite range, are not.  It also provides a starting point for considering how to create distributions that are not analytically tractable.

With the exponentially-distributed pseudorandom numbers in hand, we can then estimate the integral with the importance sampling method and compare it to using naïve uniformly-distributed Monte Carlo.  The code I used to perform this comparison is:

Ns   = [i for i in range(10,2010,10)]
xmin = 0
xmax = 10
df   = pd.DataFrame()

#exact answeer for this integral in terms of the error function
exact = np.sqrt(np.pi)/2.0*special.erf(10) 

def f(x): return np.exp(-x*x)
def pu(span): return 1/(span[1]-span[0])
def pe(x): return np.exp(-x)
def xk(x): return -np.log(1-x)

for N in Ns:
    U = np.random.random((N,))
    FU = f(xmin + xmax*U)
    PU = pu((xmin,xmax))
    XK = xk(U)
    PE = pe(XK)
    FX = f(XK)

    mean_U = np.mean(FU/PU)
    sig_U  = np.std(FU/PU)/np.sqrt(N)
    err_U  = mean_U - exact
    mean_K = np.mean(FX/PE)
    sig_K  = np.std(FX/PE)/np.sqrt(N)
    err_K  = mean_K - exact

    row = {'N':N,\
           'I_U':mean_U,\
           'sig_I_U':sig_U,\
           'error_U':err_U,\
           'I_K':mean_K,\
           'sig_I_K':sig_K,\
           'error_K':err_K}
    df  = df.append(row,ignore_index=True)

Each record of the dataframe df contains the number of Monte Carlo trials $N$ as well as the estimated value of the integral, the uncertainty for both the uniform and importance-sampled estimators, and their corresponding actual error, respectively.  The following plot shows the error in the estimated value of the integral

clearly demonstrating the superior performance of the importance sampling with the exponential distribution, which converges rapidly for small $N$ and which exhibits less tendency to fluctuate as well.  The plot of standard deviation shows similar performance

with the standard deviation in the exponential sampling falling much faster as a function of $N$ and achieving a smaller and smoother overall value.  The standard deviation, which is the only measure one has when the exact value of the integral is unknown, is often called the formal error as it is taken as a proxy for the exact error.

Next month we’ll discuss some of use cases where the estimation of high-dimensional integrals necessitates importance sampling and the high-powered algorithms that can be plugged-in (sometimes with some effort).