Category Theory Part 2 – Basics of Isomorphisms
This month’s installment continues the journey through Lawvere’s and Schanuel’s book on category theory (see last month’s installment). In that article, the basic idea of category theory emerged as a set of ‘meta-rules’ that focused not on the elements of two sets but on the mappings between those sets. In addition, the authors emphasized analogies with scientific thought and with ordinary arithmetic.
That section was rather short, though, and in this post the machinery gets to be a bit more complicated. The central theme for the second section of the book (Article II and its accompanying Sessions) centers on isomorphisms. This month’s installment will focus only on the basics of isomorphisms, with the hooks to future blogs on the topics of choice (i.e., sections of a map) and determination (i.e., retractions of a map).
It is interesting to note that a suspicion voiced in last month’s column seems to be on target: namely, that much of this work is philosophical rather than just mathematical. The first indication of this is that Lawvere and Schanuel try to motivate the concept of isomorphisms by imagining a point in humanitie’s past where the formal concept of numbers had yet to be invented. The question that they pose is, just how did man know when two things were equal?
The answer that they provide is a simple one. Humanity devoid of formal numbers would not be able to count the number of elements in a set and compare that total to the total from another to establish that the sets have the same size. But they could try to put the elements in each set into a one-to-one correspondence.
The example they construct consists of a nuclear family (father, mother, and child) and a collection of items that belong to or are identified with the person.
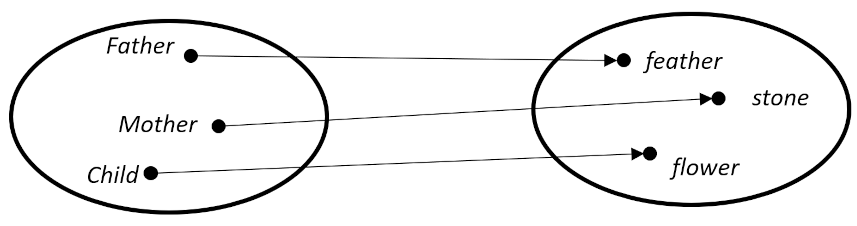
The idea is that no matter how unsophisticated the family mathematics may be, each member of this group can claim treasure all his own and, in doing so, realize that the family group is the same size as the collection of personal treasures. This example is a bit too ‘tribal’ for my taste, but it did get me thinking of those old heist movies where, after having made off with the loot, the criminals divvy up the cash using the ‘one for you, one for me’ scheme.
Be that as it may, there is an even more subtle notion lurking under the surface of this basic concept of equality. Not only does each person have a treasure to call their own, but each treasure has an owner. This bidirectionality is more special than the rules discussed in the category of sets. In the latter, the only condition on a proper mapping is that each element in the set labeled as the domain has an arrow departing from it that connects with one and only one element in the codomain. There was no condition placed on each element of the codomain connecting it back to one and only one element in the domain.
A bit of reflection should, in general, convince one to reject a requirement that an element in the codomain must connect back to the domain. Imposing such a requirement would mean that entire propositions would be impossible to express. For example, consider the set of students {Andy, Barbara, Carl, Denise} who have just taken a test, and the set of possible grade outcomes {A,B,C,D,F}.
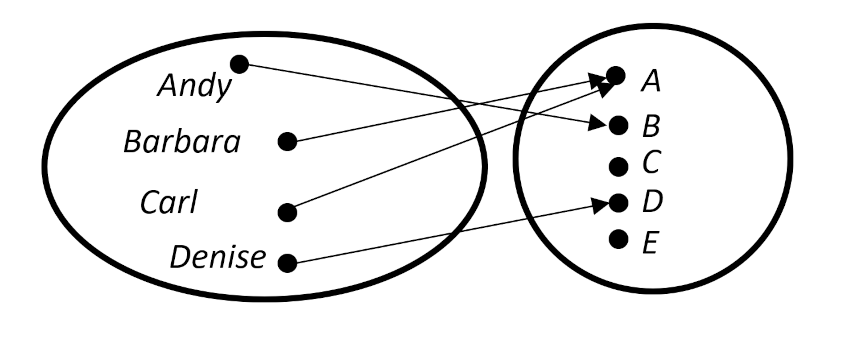
The statement “No student failed the exam” could not be encoded into the language of category theory if every grade level needed to link to a student (and only one student). (It is comical to think about a world were such a requirement were imposed. Classes could never have any number of students but 5, and then, even if the scores on a 100-point exam were 1, 2, 3, 4, and 5, the top scorer would walk away with an A.)
So, the idea that the lines connecting the domain to the codomain can, in certain classes of mapping, be reversed is quite remarkable. When a mapping possesses this bidirectionality it is called an isomorphism, and the formal definition is as follows:
A map $f: A \rightarrow B$ is called an isomorphism or invertible map, if there is a map $g:B \rightarrow A$ such that $g \circ f = I_A$ and $ f \circ g = I_B $.
Two special maps, $I_A$ and $I_B$, appear, which are the identity maps that take elements in the sets $A$ and $B$ back into themselves. The map $g$ is also special in that it is unique and so it can be, without a loss of generality, denoted as $f^{-1}$.
It might be tempting to think that having both composition rules is redundant (e.g., $g \circ f = I_A$ has the same information as $ f \circ g = I_B$) but, as the following example shows, both are needed.
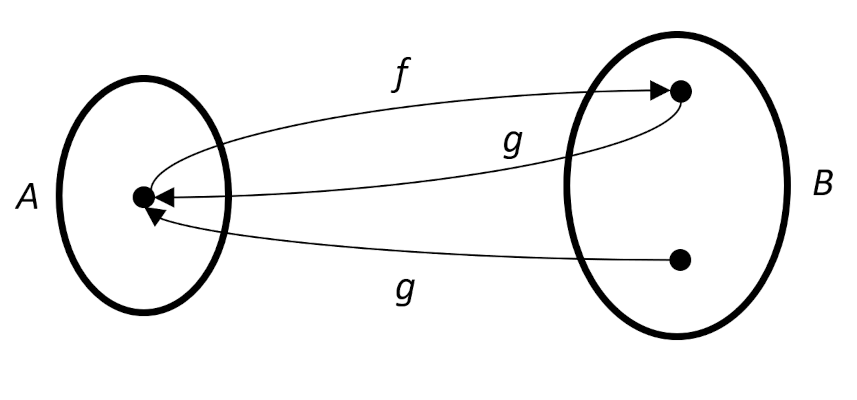
For these mappings, $g \circ f = I_A$ but $f \circ g \neq I_B$.
It’s also easy to look past this definition and think that more must be needed, but the authors soon dispel that idea as well by showing that the following associated properties follow from it – namely that an isomorphism is:
| Reflexive | $A$ is isomorphic to $A$ |
| Symmetric | If $A$ is isomorphic to $B$, then $B$ is isomorphic to $A$ |
| Transitive | If $A$ is isomorphic to $B$, and $B$ is isomorphic to $C$, then $A$ is isomorphic to $C$ |
These associated properties, and a host of other ones as well, are relatively easy to prove, but can look strange to one not used to the manipulations. The primary strategy involves introducing the identity maps (either $I_A$ or $I_B$) at opportune moments.
For example, the proof of the transitive property goes as:
- $A$ isomorphic to $B$ means $f:A \rightarrow B$ and that there is a $g: B \rightarrow A$ such that $f \circ g = I_B$ and $g \circ f = I_A$.
- $B$ isomorphic to $C$ means $h:B \rightarrow C$ and that there is a $k: C \rightarrow B$ such that $h \circ k = I_C$ and $k \circ h = I_B$.
- Then the map $h \circ f: A \rightarrow C$ (by composition).
- We now need to show that there exists an inverse map $ (h \circ f)^{-1}:C \rightarrow A$ such that $(h \circ f)^{-1} \circ (h \circ f) = I_A$ and $(h \circ f) \circ (h \circ f)^{-1} = I_C$
- From the definition of the inverse $(h \circ f)^{-1}$ must be equal to $g \circ k$.
- Putting it all together we see that:
- $(h \circ f)^{-1} \circ (h \circ f) = (g \circ k) \circ (h \circ f) = $ $g \circ (k \circ h) \circ f = I_B = ( g \circ I_B) \circ f = g \circ f = I_A$
- $(h \circ f) \circ (h \circ f) ^{-1} = (h \circ f) \circ (g \circ k) = $ $h \circ (f \circ g) \circ k = h \circ I_B \circ k = h \circ (I_C \circ k) = h \circ k = I_C$
Next month we’ll look at an equivalent definition of an isomorphism that has analogies to division in arithmetic using the concepts of sections and retractions of maps.
