Category Theory Part 4 – Determination and Choice
This month’s post on category theory picks up where the last post left off, with a look at the choice problem, the complimentary situation in map composition to the determination problem considered in the last post. However, before digging in the choice problem directly this narrative will begin by revisiting the determination problem. This go-back is one of the consequences of just following where the roots of discovery lead without having trampled down a path. After having a month to reflect on the determination problem, it became clear that a discussion of the choice problem would greatly benefit from a little more detail in former.
One of the major failures of Lewvere’s and Schanuel’s book is not sufficiently connecting the combinatorics associated with composing maps with both problems. While it is true that the text emphasizes the formal analogies between multiplication of ordinary numbers with compositions of maps, the usefulness of the analogy is never clearly stated. Their exposition goes from the very simplistic (e.g. considering how to tell when two sets have the same number of elements) to the very complicated (retractions and sections as a way of defining inverse mappings) with no intermediary steps. The purpose of this post is to provide those waypoints. Along the way, it will become clearer why the authors focus on automorphisms.
To lay the groundwork, consider the finite sets $A$, $B$, and $C$ as shown in the diagram below,
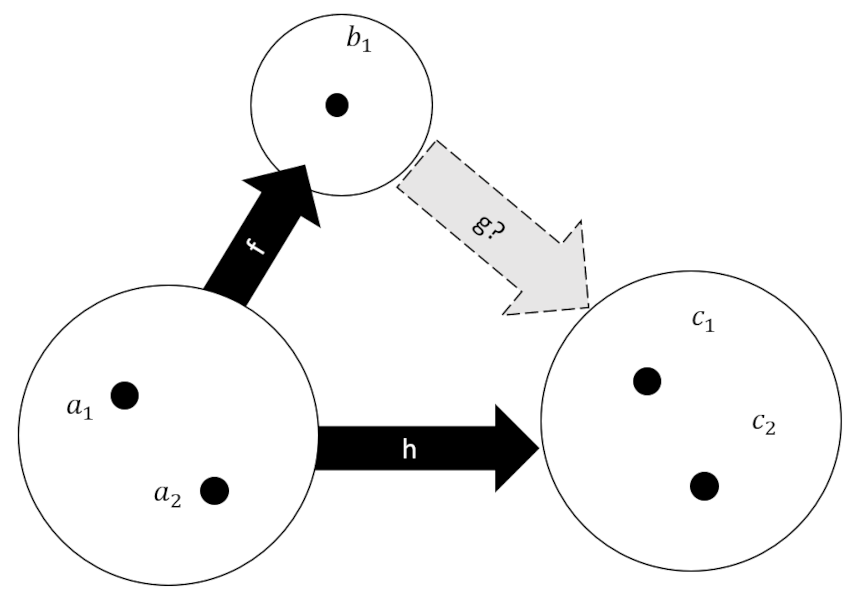
along with known mappings $f:A \rightarrow B$ and $h:A \rightarrow C$ and the yet-to-be-determined mapping $g:B \rightarrow C$. Set $A$ has two elements as does $C$, while $B$ has only one. In the last post, the importance of the mapping $f$ being injective was raised but not sufficiently explained. A clear distinction wasn’t made as to whether or not a non-injective map could actually solve the determination problem. We will detail the various mappings possible between the three sets shown in the figure and will show that not injective mappings can solve the determination problem but only in special contrived cases and never when the mapping between $A$ and $C$ is an automorphism.
Before diagraming each of the individual cases, let’s count the number of diagrams needed – one for each of possible sets of mappings ${f,g,h}$ (whether or not the set solves the determination problem). The number of mappings between any two sets is equal to the number of elements in the target or codomain set raised to the power of the number of elements in in the domain set. Since $B$ has only one element all mappings from any other set must look the same, that is every element of the domain maps to the singleton in $B$. The number of mappings from $B$ to $C$ is equal to the number of elements in $C$, which in this case is two. A similar computation shows that the number of distinct mappings from $A$ to $C$ is four. Already we can see that there is likely to be a problem in trying to solve the determination problem as there are only two distinct ways to go from $A$ to $C$ with a waypoint at $B$ whereas there are four ways in which to go from $A$ to $C$ directly. To see which of the four versions of $h$ are incompatible let’s look at the diagrams for the cases where $h$ is not injective followed by where it is.
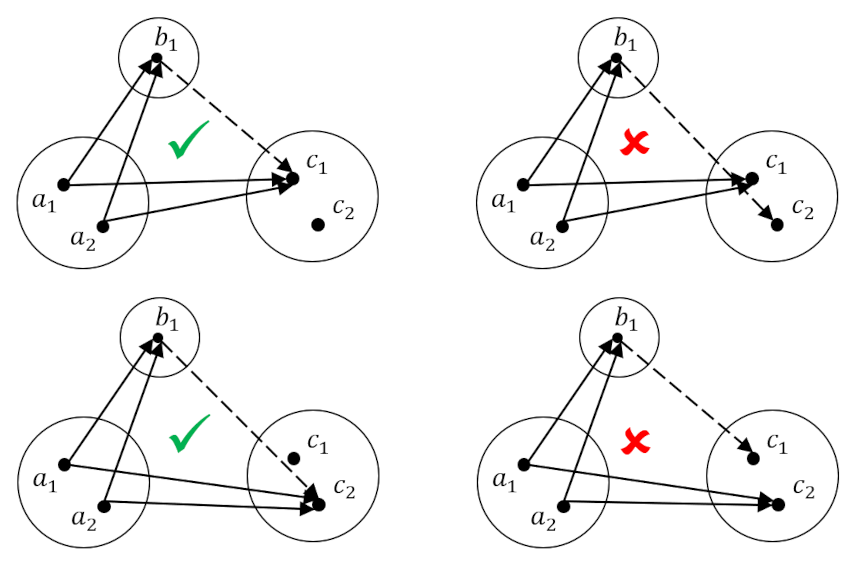
In the case were the mapping $h:A \rightarrow C$ is not injective, there is always the solution to the determination problem despite the fact that the mapping from $f:A \rightarrow B $ also fails to be injective. The figure below shows the four possible sets of ${f,g,h}$ in this case with the left side showing the correct choice for the mapping $g$ and the right showing the wrong way to do it.
However, when the mapping $h$ is injective, that is to say that each element in $A$ maps to a unique element in $C$ (more generally every point in the codomain has, at most, one incoming arrow), then no solution to the determination problem can be found. This is shown in the following diagram for the two distinct possibilities for $h$, one of which is in an automorphism (with the identifications $a_1 = c_1$ and $a_2 = c_2$) and the other a permutation.
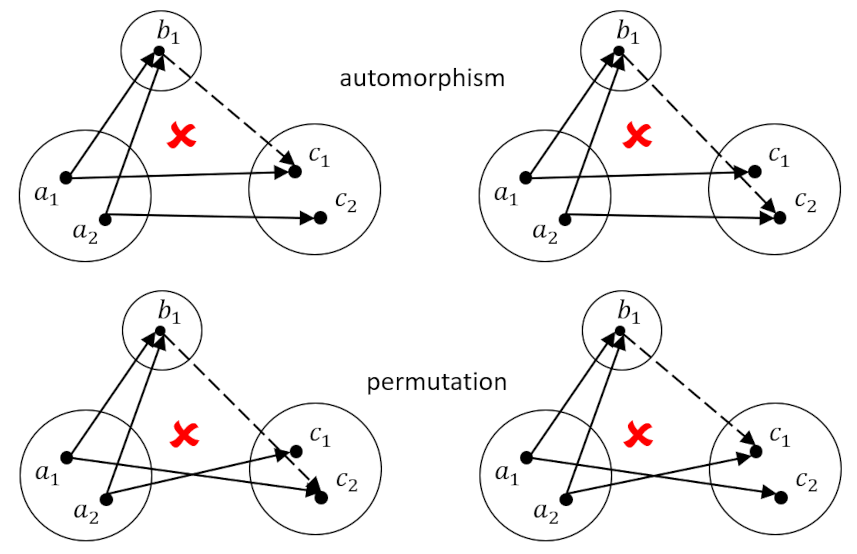
If we restrict ourselves to only the automorphism between $A$ and $C$, then we have to give up all hope of contriving a solution if $f$ is not injective, because, otherwise we would have to force some doubly-targeted element (i.e. $b_1$ in this case) into trying to do the impossible – to simultaneously point to two separate elements in its codomain.
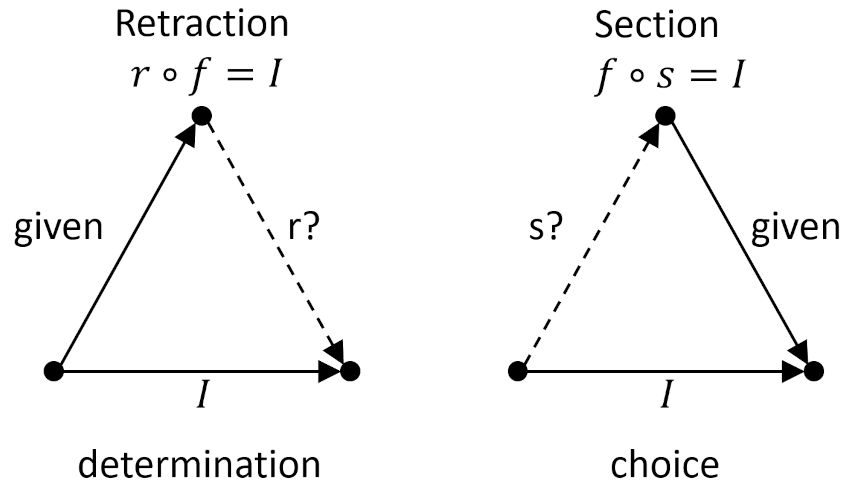
The special case where a mapping $g$ solves the determination problem for the case where $h=I_A$ is called a retraction for $r$ for $f$ and it obeys the relation $r \circ f = I_A$.
We are now in a better position to understand the choice problem and the role of the automorphisms in it. The choice problem is the analog to the determination problem where the mappings $h: A \rightarrow C$ and $g:B \rightarrow C$ are known and where the map being sought is $f:A \rightarrow B$. We’ve already cataloged all the possible sets of maps in the examples above and we know that the choice problem is only compatible with the case where $h$ is not-injective but this doesn’t give us enough information to understand the properties of $g$. So, to really appreciate the choice problem we are going to have to change the composition of the sets. The simplest approach is to enlarge $B$ to have 3-elements (the reason for skipping a 2-element $B$ should become obvious afterwards).
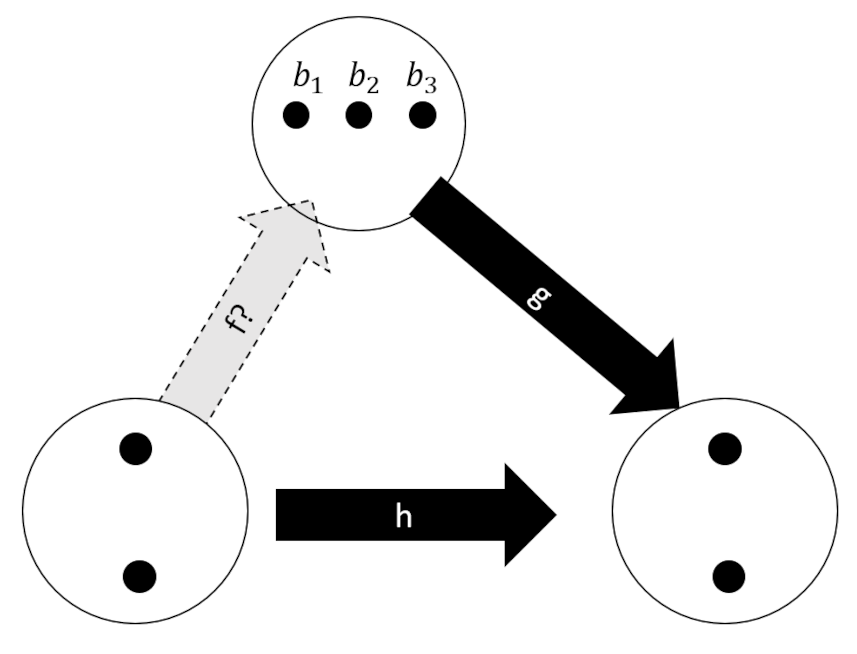
Since we are interested in automorphisms as a special case of the 4 possible mappings from $A$ to $C$ we can substantially decrease the tedium of working through all the possible combinatorics. In this special case, a solution to the choice problem is called a section and is usually denoted as $s$.
Despite this simplification, there are still nine possible mappings into $B$ and eight possible mappings from it (for a total of 72 possibilities). Fortunately, our job will get even easier after we examine the following diagram which focuses on one specific mapping from $B$.
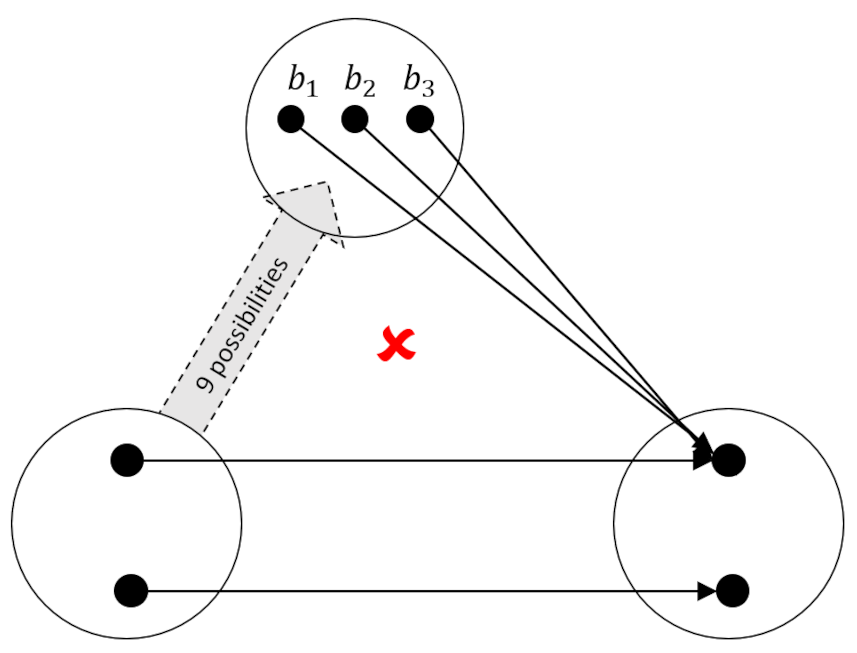
Of the nine possibilities that map the 2-element set (call it $A$ or $C$ as you wish) to $B$ none of them work because each element of $B$ aims at the same element in $A$. The remedy is to make sure that mapping $g$ sends at least one arrow to each element in $C$ – that is that $h$ is surjective.
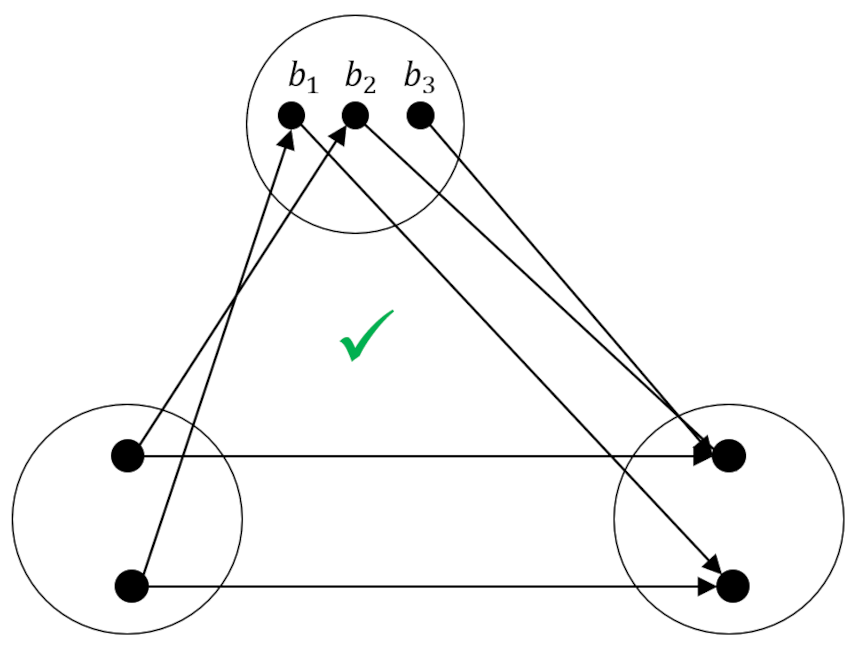
It doesn’t matter exactly how the rest of the mapping is specified (for example $b_3$ could point to the other element). The key feature is simply that all elements in $A$ are covered with at least on arrow head.
These two special cases are summarized quite nicely in the following diagram (adapted from the one on page 73 of Lawvere and Schanuel).
Next month, we’ll explore how to relate retractions and sections of a given map $f$ to a variety of ‘division problems’ in the category of finite sets and will we’ll explore a new insight into inverse mappings $f^{-1}$ that they provide.
