Monte Carlo Integration – Part 5
This month we examine some of the specialized algorithms and packages that have been developed over several decades to perform importance sampling in a variety of scenarios. Before digging to the specifics, it is worth setting the stage as to why importance sampling is such a key part of many problems.
A number of fields deal with high dimensional integrals. Most likely, the original scenarios involving such integrals came about in connection to many-particle physics. They arise in computing so-called loop corrections to quantum field theories which have the form
\[ I = \int d^3 k_1 d^3 k_2 \ldots d^3 k_n f({\vec k}_1, {\vec k}_2, \ldots ,{\vec k})_n \; , \]
where the ${\vec k}_i$ are the spatial momenta for the $i^{th}$ particle involved. Likewise, the classical statistical description of the motion of group of $N$ particles involves computing the partition function given by
\[ Z = \int d^3 q_{(1)} d^3 p^{(1)} \ldots d^3 q_{(N)} d^3 p_{(N)} f(q^{i}_{(1)},p_{j}^{(1)},\ldots, q^{i}_{(N)},p_{j}^{(N)} ) \; , \]
where the $q^{i}_{(J)}$ and $p_{i}^{(J)}$ are the generalized coordinates and momenta for the $J^{th}$ particle and $f$ describes the interaction.
In more recent years, high dimensional integrals have found a place in modeling images (ray tracing, path tracing, and production rendering) and in mathematical finance, to name only a few.
Clearly, any system with sufficiently high number of continuous degrees of freedom is apt to birth an integral that has more dimensions than what can be efficiently dealt with using the more traditional structure quadrature methods – hence the need for Monte Carlo. What is not so obvious is that, generically, the integrands are likely to be tightly peaked in only a small fraction of the total volume – hence requiring importance sampling.
This later point is typically easier to understand with a simple example in which we estimate the percentage of the volume of unit width consume by a sphere of unit diameter inscribed in the box. In one dimension, the box extends over the range $[-0.5,0.5]$ and the sphere, defined as all the points within a distance of $0.5$ from the origin, are coincident. The 1-sphere has two points where it touches the edge and there are no corners outside and thus it consumes 100% of the volume of the inscribing box. In two dimensions, the box extends of the range $[-0.5,0.5]$ along two axes and the 2-sphere has volume $V = \pi (0.5)^2$. There are four points where the 2-sphere touches the edge of the box and there are four corners that lie outside. The 2-sphere only consumes 78.5% of the volume of the box. In three dimensions, the volume of the 3-sphere is $V = 4\pi/3 (0.5)^2$ leaving 8 corners to lie outside and only 52.8% of the volume consumed. A compact generalized formula for the volume of sphere in $N_D$-dimensions is given by
\[ V_{N_D} = \frac{\pi^{N_D/2}}{\Gamma \left(\frac{N_D}{2} + 1 \right)} \; .\]
The following plot shows just how quickly the volume fraction plummets to zero as the number of dimensions increases.
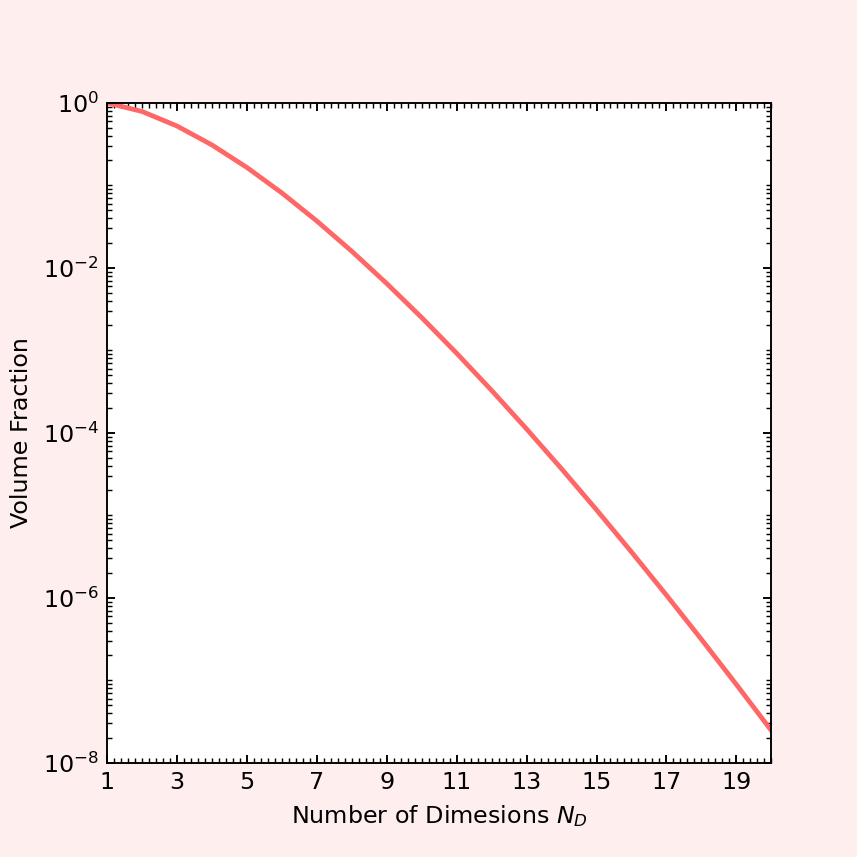
At $N_D=20$ the 20-sphere touches all $2^20$ faces of the box but only at one point thus failing to include the $2^20$ corners containing points with distances greater than $0.5$ from the origin leading to an amazingly small percentage (0.0000025%) of the total volume occupied. So, even in a scenario where the integrand seems ‘spread out’ the important region of the function is strongly peaked.
It is against this backdrop that we find several multi-purpose Monte Carlo importance sampling algorithms.
Perhaps the oldest and most revered algorithm is VEGAS authored by G. Peter LePage in 1978. VEGAS, which has its roots in particle physics, works by first ‘feeling out’ the integrand, looking for regions where the integrand is large in magnitude. The algorithm grids the space coarsely to begin with and samples the function to make a histogram. It then refines the sampling along each coordinate direction but avoids the combinatoric issues associated with structured quadrature by assuming that the integrand is separable in the sense that
\[ f(x_1, x_2, \ldots) = f_1(x_1) f_2(x_2) \ldots \; . \]
Having identified those regions with this adaptive gridding, VEGAS then concentrates the subsequent Monte Carlo trials using importance sampling to produce an estimate of the integral with an approximately minimized variance.
Roughly two decades after the release of VEGAS, Thorsten Ohl proposed an improvement to VEGAS in his paper entitled Vegas Revisited: Adaptive Monte Carlo Integration Beyond Factorization, in which he addresses the assumption that the integrand is separable. Ohl found that his algorithm VAMP “show[ed] a significantly better performance for many ill-behaved integrals than Vegas.” It isn’t clear how widely accepted VAMP has become but clearly some of the improvements that VAMP sought to add to VEGAS have been included in the new version of called VEGAS+. Lepage’s article Adaptive Multidimensional Integration: VEGAS Enhanced describes the improvements in VEGAS+ over classic VEGAS, including a new adaptive stratified sampling algorithm. Lepage provides both a free software python package on GitHub and comprehensive documentation. Stratified sampling is a complementary method to importance sampling where the Monte Carlo samples are preferentially placed in regions where the integrand changes rapidly rather than strictly in regions where its magnitude is large. The classic algorithm in stratified sampling is MISER but discussing it is out of scope in this analysis of importance sampling. Suffice to say that both VEGAS and MISER are sufficiently important that they the only Monte Carlo algorithms packaged in the GNU scientific library.
