States, Abstraction, and Implicit Objects
This post grew out of a conversation in which I recently participated, about the correct way to computationally model a system. The conversation covered the usual strategies of identifying the system’s states and how to abstract the appropriate objects to hold or contain the states based on the question at hand. But what was most interesting were the arguments put forward about the importance of recognizing not only the explicit objects used in the modeling but also the implicit objects that were ignored.
By way of a general definition, an implicit object is an object whose existence is needed in the computer modeling of the system in question but one that is not represented in code as either a real or virtual class. I don’t think this definition is used in computer science or programming books but it should be. This is a point that is almost entirely ignored in the field but is vital for a correct understanding of many systems.
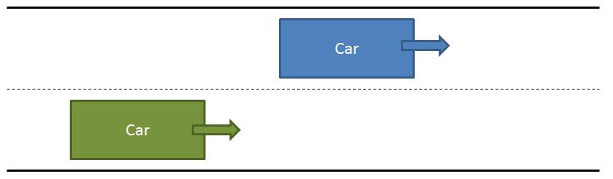
A simple example will go a long way to clarify the definition and to also raise awareness that implicit objects are used more often than people realize. The system to be modeled is the motion of traffic on a highway. For simplicity, we’ll focus on two cars, each traveling along a straight stretch of road. Generalizations to more complicated situations should be obvious but don’t add anything to the discussion. A picture of the situation is
Here we have a blue car and a green car moving to the right as denoted by the matching colored arrows. The typical abstraction at this point is to create a car class with appropriate attributes and member functions for the questions we want to answer. Let’s suppose that we are interested in modeling (with an eye towards prevention) the collision between the two cars. What ingredients are needed to perform this modeling?
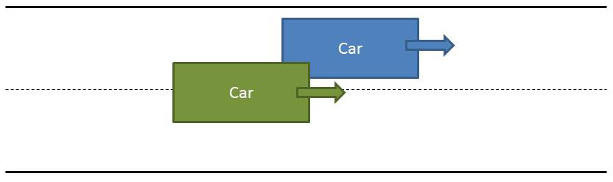
A collision between two objects occurs, by definition, when they try to occupy the same space at the same time. Unpacking this sentence leads us to the notion of position for each car as a function of time and a measure of the physical extent of each car. Collision occurs when the relative position between the centers of the two cars is such that their physical extents overlap.
Now, real life can be rather complicated, and this situation is no different. The physical shape of a car is generally hard to model with many faces, facets, and extrusions. And the position of the car is a function of what the driver perceives, how the driver reacts, and how much acceleration or deceleration the driver imposes.
In time-honored fashion, we will idealize the cars as having a simple two-dimensional rectangular shape as shown in the figure, and will also assume that the cars have a simple control law (which we don’t need to specify in detail here except to say that it depends on the position, velocity, and time) that gives the velocity of the car at any instant of time. With these simplifying assumptions, the trajectory of the car is completely specified by giving its position at some initial time and then using the control law to update the velocity at each time step. The position is then updated using the simple formula ${\vec x}(t+dt) = {\vec x}(t) + {\vec v} dt$.
With all these data specified, we might arrive at a class definition for the car object that looks like:
At this point, we’ve already encountered our first two implicit objects.
The first one is a coordinate frame, comprised of an origin and an orientation of the coordinate axes, which tells us what the position of the object is measured against. This coordinate frame is an object in its own right and, in many circles, worthy of study. Here it is simply important to acknowledge that it exists and that the width and length parameters need to be defined consistently with regards to it. This is an important point, since a change in coordinate frame orientation will change the test (to be described later) for the geometric condition of overlap (i.e., collision).
The second implicit object is much more subtle and it took the discovery of the principles behind special relativity to drive that point home. Both cars share a common clock to describe their motion. That is to say that their velocities are only meaningfully compared if their clocks are synchronized and ticking at the same speed. The role of the implicit clock is usually carried out by the main program of the simulation but, since each object holds its own time, care must be exercised to keep them synchronized. It is possible to make this common-clock assumption stronger by eliminating time from the list of member data, but that approach also has its drawbacks, as will be touched on below.
The final question is, how do we determine if the cars collide somewhere during the simulation? There are two possible approaches. The first is that we give each car a new member function, called detect_collision, which takes as arguments the position of the other car and its size. This is not an unreasonable approach for simple situations, but it quickly becomes unwieldy should we later want to add fidelity to the simulation. For example, if we wanted to allow for the body of the car changing its orientation as it changes lanes, then the number of parameters that we have to hand into the detect_collision function has to increase. A more robust way to do this is to perform this computation at the main workspace in the simulation. If this method is chosen, we’ve now introduced a third implicit object. It’s not quite clear from the context what to call this object, but it’s function is absolutely clear – it communicates to the world the message that the two cars have collided.
This last notion may seem like a trivial observation leading to an unnecessary complication but consider the case where each car is equipped with some sensor that warns of an eminent collision. Remote sensing requires some model of the medium between the sensor and thing being sensed. If the collision detector uses sound, then the air between the cars must be modeled as an elastic medium, with a finite propagation speed of the signal, and variations in this medium due to temperature, humidity, and the like may need also need to be modeled. If the collision detector uses electromagnetic waves (radar or laser ranging), then the index of refraction and dispersion properties of the air become the key parameters that again may depend on the thermodynamics of the atmosphere. In either case, this communicating medium now must be promoted from an implicit object to an explicit one and the times of the two objects take on new meaning as we need to track the transmit and receive times of the signals sent between them.
The lesson, I hope, is clear. It is just as important to pay attention to the implicit objects in a simulation as it is to the explicit ones. There is a parallel here with the spoken word – where it is often as important to pay attention to what was left unsaid as it is to what was said.