This week’s column has a three-fold inspiration. First off, most of the most exciting and controversial philosophical endeavors always involve arguing from incomplete or imprecise information to a general conclusion. These inferences fall under the heading of either inductive or abductive reasoning, and most of the real sticking points in modern society (or any society for that matter) revolve around how well a conclusion is supported by fact and argument. The second source comes from my recent dabbling in artificial intelligence. I am currently taking the edx course CS188.1x, and the basic message is that the real steps forward that have been taking shape in the AI landscape came after the realization was made that computers must be equipped to handle incomplete, noisy, and inconsistent data. Statistical analysis and inference deals, by design, with such data, and its use allows for an algorithm to make a rational decision in such circumstances. The final inspiration came from a fall meeting of my local AAPT chapter in which Carl Mungan of the United States Naval Academy gave a talk. His discussion of the two aces problem was nicely done, and I decided to see how to produce code in Python that would ‘experimentally’ verify the results.
Before presenting the various pieces of code, let’s talk a bit about the problem. This particular problem is due to Boas in her book Mathematical Methods for the Physical Sciences, and goes something like this:
The first part of this three-fold problem is very well defined and relatively simple to calculate. The second two parts require some clarification of the phrase ‘is known to be’. The first possible interpretation is that the player separates out the aces from the deck and either chooses one of them at random (part 2) or he chooses the ace of spades (part 3). He returns the remaining 3 aces to the deck, which he subsequently shuffles prior to drawing the second card. I will refer to this method as the solitaire option. The second possible interpretation (due to Mungan) is that a dealer draws two cards at random and examines them both while keeping their identity hidden from the player. If one of the cards is an ace (part 2) or is the ace of spades (part 3), the dealer then gives the cards to the player. Parts 2 and 3 of the question then ask for the probability that the hands that pass this inspection step actually have two aces. Since this last process involves assistance from the dealer, I will refer to it as the assisted option. Finally, all probabilities will be understood from the frequentist point of view. That is to say that each probability will be computed as a ratio of desired outcomes to all possible outcomes.
With those preliminary definitions out of the way, let’s compute some probabilities by determining various two-card hand outcomes.
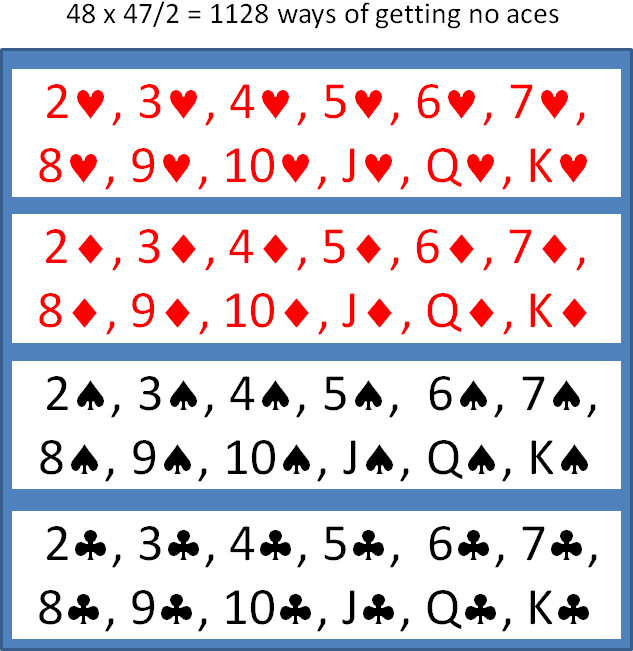
First let’s calculate the number of possible two-card hands. Since there are 52 choices for the first card and 51 for the second, there are 52×51/2 = 1326 possible two-card hands. Of these, there are 48×47/2 = 1128 possible two-card hands with no aces, since the set of cards without the aces is comprised of 48 cards. Notice that, in both of these computations, we divide by 2 to account for the fact that order doesn’t matter. For example, a 2 of clubs as the first card and a 3 of diamonds as the second is the same hand as a 3 of diamonds as the first card and a 2 of clubs as the second.
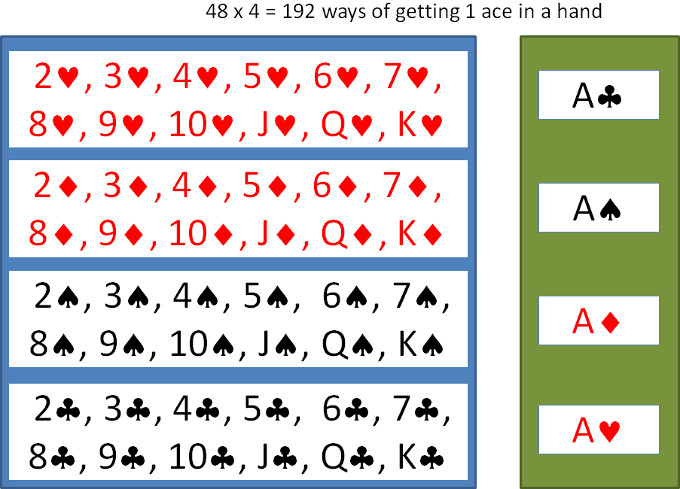
Likewise, there are 48×4 = 192 ways of getting a hand with only 1 ace. Note that there is no need to divide by 2, since the two cards are drawn from two different sets.
Finally, there are only 6 ways to get a two-ace hand. These are the 6 unique pairs that can be constructed from the green set shown in the above figure.
As a check, we should sum the size of the individual set and confirm that it equals the size of the total number of two-card hands. This sum is 1128 + 192 + 6 for no-ace, one-ace, and two-ace hands, and it totals 1326, which is equal to the size of the two-card hands. So, the division into subsets is correct.
With the size of these sets well understood, it is reasonably easy to calculate the probabilities asked for in the Boas problem. In addition, we’ll be in a position to determine something about the behavior of the algorithms developed to model the assisted option.
For part 1, the probability is easy to find as the ratio of all possible two-ace hands (6 of these) to the number of all possible two-card hands (1326 of these). Calculating this ratio gives 6/1326 = 0.004525 as the probability of pulling a two-ace hand from a random draw from a well-shuffled standard deck.
For parts 2 and 3 in the solitaire option, the first card is either given to be an ace or the ace of spades. In both cases, the probability of getting another ace is the fraction of times that one of the three remaining aces is pulled from the deck that now holds 51 cards. The probability is then 3/15 or 0.05882.
The answers for the assisted option for parts 2 and 3 are a bit more subtle. For part 2, the dealer assists by winnowing the possible set down from 1326 possibilities associated with all two-card hands, to only 192 possibilities associated with all one-ace hands, plus 6 possibilities associated with all two-ace hands. The correct ratio is 6/198 = 0.03030 as the probability for getting a single hand with two aces when it is known that one is an ace. For part 3, the dealer is even more zealous in his diminishment of the set of possible hands with one card, the ace of spades. After he is done, there are only 51 possibilities, of which 3 are winners, and so the correct ratio is 3/51 = 0.05882 as the probability of getting a single hand with two aces when it is known that one is the ace of spades.
All of these probabilities are easily checked by writing computer code. I’ve chosen python because it is very easy to perform string concatenation and to append and remove items from lists. The basic data structure is the deck, which is a list of 52 cards constructed from 4 suits (‘S’,’H’,’D’,’C’), ranked in traditional bridge order, and 13 cards (‘A’,’2’,’3’,’4’,’5’,’6’,’7’,’8’,’9’,’10’,’J’,’Q’,’K’). Picking a card at random is done importing the random package and using random.choice, which returns a random element of a list passed into it as an argument. Using the random package in the code turns the computer modeling into a Monte Carlo simulation. For all cases modeled, I input the number of Monte Carlo trials to be N = 1,000,000.
Code to model part 1 and parts 2 and 3 for the solitaire option is easy to implement and understand, so I don’t include it here. The Monte Carlo results (10 cases each with N trials) certainly support the analysis done above, but, if one didn’t know how to do the combinatorics, one would only be able to conclude that the results are approximately 0.0045204 +/- 0.00017.
The code to model parts 2 and 3 for the assisted option is a bit more involved because the dealer (played by the computer) has to draw a hand then either accept or reject it. Of the N Monte Carlo trials drawn, what percentage of them will be rejected? For part 2, this amounts to determining what the ratio of two-card hands that have at least one ace relative to all the possible two-card hands. This ratio is 192/1326 = 0.1448. So, roughly 85.5 % of the time the dealer is wasting my time and his. This lack of economy becomes more pronounced when the dealer rejects anything without an ace-of-spades. In this case, the ratio is 51/1326 = 1/52 = 0.01923, and approximately 98% of the time the dealer is throwing away the dealt cards because they don’t meet the standard. In both cases, the Monte Carlo results support the combinatoric analysis with 0.03031 +/- 0.0013 and 0.05948 +/- 0.0044.
import random
suits = ['S','H','C','D']
cards = ['A','2','3','4','5','6','7','8','9','10','J','Q','K']
def make_deck():
deck = []
for s in suits:
for c in cards:
deck.append(c+s)
return deck
def one_card_ace(num_mc):
num_times = 0
num_good = 0
deck = make_deck()
for i in range(0,num_mc,1):
card1 = random.choice(deck)
deck.remove(card1)
card2 = random.choice(deck)
deck.append(card1)
if card1.find('A') == 0 or card2.find('A') == 0:
num_times = num_times + 1
if card1.find('A') == 0 and card2.find('A') == 0:
num_good = num_good + 1
print deck
return [num_times, num_good]
def ace_of_spades(num_mc):
num_times = 0
num_good = 0
deck = make_deck()
for i in range(0,num_mc,1):
card1 = random.choice(deck)
deck.remove(card1)
card2 = random.choice(deck)
deck.append(card1)
if card1.find('AS') == 0:
num_times = num_times + 1
if card2.find('A') == 0:
num_good = num_good + 1
print deck
return [num_times,num_good]
Notice that the uncertainty in the Monte Carlo results grows larger in part 2 and even larger in part 3. This reflects the fact that the dealer only really affords us about 150,000 and 19,000 trials of useful information due to the rejection process.
Finally, there are a couple of philosophical points to touch on briefly. First, the Monte Carlo results certainly support the frequentist point of view, but they are not actual proofs of the results. Even more troubling is that a set enumeration, such as given above, is not a proof of the probabilities, either. It is a compelling argument and an excellent model, but it presupposes that the probability should be calculated by the ratios as above. Fundamentally, there is no way to actually prove the assumption that set ratios give us the correct probabilities. This assumption rests on the belief that all possible two-card hands are equally likely. This is a very reasonable assumption, but it is an assumption nonetheless. Second, there is often an accompanying statement along the lines that, the more that is known, the higher the likelihood of the result. For example, knowing that one of the cards was an ace increased the likelihood that both were an ace by a factor of 6.7. While true, this statement is a bit misleading, since, in order to know, the dealer had to face the more realistic odds that 82 percent of the time he would be rejecting the hand. So, as the player, our uncertainty was reduced only at the expense of a great deal of effort done on our behalf by another party. This observation has implications for statistical inference that I will explore in a future column.