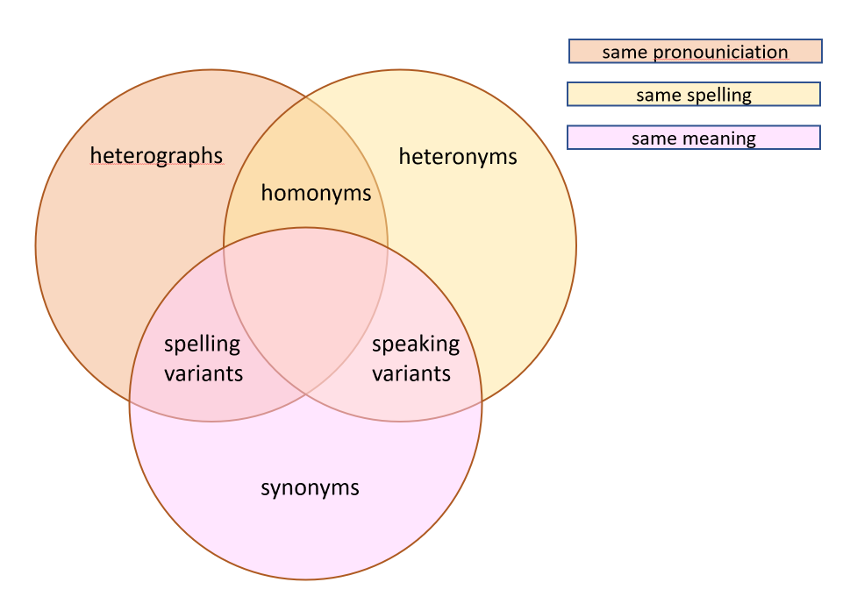
Pseudoscience and Science?
The roots of this post date back almost over three decades. Shortly after I started full time employment and had some money to spend I decided to get a subscription to Scientific American. At the time, I thought that it was a excellent publication devoted to pure science. With time I began to see the business side of it, the need to generate ‘science excitement’ even when there was perhaps none. Over the years, I became much more savvy in seeing the ebb and flow, the highs and the lows of their editorial policy. And I learned as much, or even more, by the bad treatments as I did from the good ones, since the former challenge one’s ability to identify, isolate, and explain what went wrong.
One particular low, which caused me to let my subscription lapse, was a provocative piece on pseudoscience. In principle, I have no beef with anyone taking sloppy thinking and evidence-poor arguments to task. I have had, on many occasions, the need to roll up my intellectual sleeves and rip apart poor scientific logic, whether it was someone else’s (I’ll discuss a particularly interesting example later on) or my own. But that’s not what the author did. Rather than focus on the ‘truth content’ of the claims, he focused on the ‘stupidity’ of the ideas and made light of those who held them and I have a big problem with that.
As a typical example, the author mocked the concept of alien abduction. You may be remarking to yourself that alien abduction should be mocked; just look at the people who assert that they are victims. But we shouldn’t be mocking people in general nor should we mock an idea, no matter how far-fetched. The assertion that people are taken off the earth and placed on alien spacecraft and are subjected to who knows what else is neither a scientific statement nor unscientific one; it is ascientific.
Admittedly, the word ‘ascientific’ is one that I’ve coined for this discussion but I think it serves the need well. No simple statement that can be uttered, such as ‘the sky is blue’ or ‘the sky is red’, can have any scientific content, merely truth content. We add the ‘science’ to these assertions by the way we investigate the claim made in the statement. In other words, the word science should mean the process by which we add a truth content to an assertion not the truth of the assertion itself.
The ‘science’ begins by the very obvious but often forgotten steps of formulating a question and then gathering what evidence exists. (The wikipedia article on the scientific method is amazingly detailed and explanatory on these points as well as the others that span the general principles of the method). In the case of alien abductions, we start with the claim at face value and look at what evidence exists. Admittedly, the evidence that its proponents muster is the worst kind of evidence, riddled with eyewitness testimony and scant bits of circumstantial evidence and no reasonable analysis would it.
So, based on the evidence, we can conclude that there is no support for the statement ‘alien abductions take place’ and the truth content of any claiming victims is low. But it doesn’t mean we disproved the statement as a whole, anymore than Europeans of nearly 350 years ago could have proved that the statement ‘some swans are white’ as false. The tests we set a limit on the likelihood of the particular assertions that have been made.
To be more concrete, I’ll draw from personal experience and talk about two of my encounters with people who believed in the explanatory and predictive power of astrology. Both of these encounters occurred when I work for a small technology firm and the people involved were highly trained STEM professionals (oddly enough they didn’t know each other). Once the individual in question brought up their belief in astrology I thought I would put the power of the system to a test. Rather than reveal my ‘star sign’ and get a stream of vague statements that could be interpreted in just about anyway, I asked for the person to predict my astrological sign given what they knew about my behavior, attitudes, and habits. In both cases, the adherent started by suggesting what I might be and eventually ruling out the actual sign under which I was born. They might have had better odds simply by spinning a zodiac spinner.
In both of these areas (alien abduction and astrological predictions), we are on firm ground saying that since we’ve examined a large number of such claims and found little to no evidence supporting them that it is unlikely we will ever find anyone with a credible set of facts that support these claims. But we need to recognize that: 1) are conclusions are not deductive proof but merely the product of statistical inference, and 2) the individuals making these claims are real people and we must treat them with rudimentary respect if we ever hope to persuade them that these positions are very likely wrong..
Now some might suggest that I’m splitting hairs with this fine distinction between the claim and the truth of the claim? What practical implications could warrant such a careful treatment? One prominent example springs to mind – the debate over whether to vaccinate.
Before digging in, let me state categorically that in my opinion the benefits of vaccines outweighs their risk and I endorse getting children vaccinated. But I am not ignorant of the fact that in the current debate there are actually two pseudoscience positions. The first is the obvious position taken by in this debate by the anti-vaccine crowd, best attested to by the recent and ongoing outbreak of measles in the US. The other pseudoscience position is by the medical professionals who assert that vaccines are perfectly safe by citing ‘medical studies’.
Much of what passes for medical studies, or statistical studies in most disciplines for that matter, themselves border on pseudoscience. As William Wilson so nicely puts it in his opening paragraph in the May 2016 article of First Things: “The problem with science is that so much of it simply isn’t.” In a nutshell, his points are that most studies are unreproducible (and therefore unfalsifiable) and are built on the flimsiest of statistical interpretation.
The public is aware of these problems even if they are unable to articulate their concerns precisely in a way that would make a philosopher happy. Therefore, it is hardly a surprise when they hold pseudoscientific positions that cause unneeded misery and death. The science community needs to put its own house in order by raising standards on publication before turning its critical eye somewhere else.