Farming To Infinity and Beyond
One of the most remarkable aspects of the human mind is its ability to work with, through imagination and insight, concepts that can’t be worked with in the material world. Nowhere is this more profoundly applied than in the synthesis of human knowledge dealing with the concept of infinity in modern mathematics.
The idea of infinity is the concept of an inexhaustible process that is imagined to be repeated as many times as desired. It is truly amazing that the human mind can abstract what would happen in a particular set of circumstances that can never be realized in the physical world.
Perhaps no scenario illustrates the simple way that insight, imagination, and intuition can be harnessed to deal with infinity than the farmer’s problem.
I must confess that while the particulars of the farmer’s problem presented below are my own, the basic framework came from a popular book on mathematics. Unfortunately, I don’t recall where I found this illustration of the power of infinity so many years ago and so I can only apologize to my source for my forgetfulness and ignorance.
The farmer’s problem can be framed as follows. Suppose that a farmer and his family – his wife and two children – decide to relocate to an off-world colony somewhere in a distant star system. Since space travel limits the amount of stuff that can be transported, our farmer – let’s call him Farmer Lister – wants to be as economical as possible. In particular, he would like to take the minimum amount of grain necessary to get his farm producing the food he and his family needs. Taking more than needed deprives them of space to take other needed resources, like farm equipment, first-aid supplies or the like.
Agricultural reports indicate that the soil on the colony world is conducive to growing wheat, and that a high-yield wheat that produces 3 bushels at harvest for each bushel planted is the optimal choice, based on soil chemistry and climate. Each colonist family brings the essential supplies to get the farm started as well as rations for the first year as the crop grows. At harvest, Farmer Lister needs to have a crop of 3 bushels in order to feed his family in the next year. The question is, then, how much wheat should he pack?
Let’s try out a couple of scenarios.
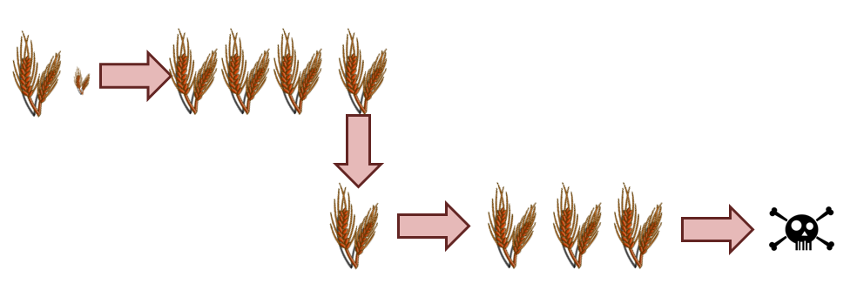
First suppose that he packs 1 bushel of wheat. During year 1 things are fine as the family plants the first bushel and eats the rations while the crop grows. At harvest, they get 3 bushels of wheat which will support them during year 2 but with nothing left over to plant for subsequent years.
Next suppose that he packs 1+1/3 bushel of wheat, which he plants during year 1. The 1 bushel of wheat produces the 3 bushels his family needs to survive year 2 and the 1/3 bushel produces an extra bushel of wheat for planting in year 2. The survival needs of year 3 are assured but tragically that is where the process stops since the 1 bushel produces only enough for food during year 3 and the Lister family dies of starvation after that.
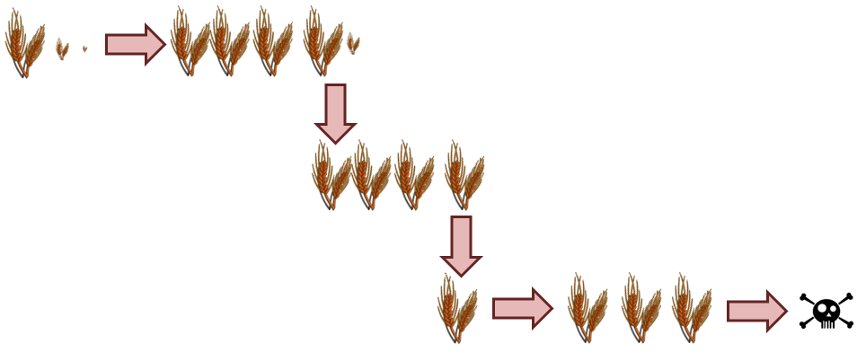
Finally, consider what happens if he adds an additional 1/9 bushel. During year 1 he plants 1 + 1/3 + 1/9 bushels and gets 3 + 1 + 1/3 bushels at harvest. During year 2, his family eats the 3 bushels and plants the 1 + 1/3 bushels for the future. At harvest, the crop yields 3 + 1 bushels. During year 3 his family eats the 3 bushels and plants the 1. At harvest, this last crop yields the 3 bushels they need to eat during year 4 but they get no further.
Clearly he is on the right track but needs to augment the initial supply by a power of 1/3 for each additional year (1/81 to have something to plant in year 4, 1/243 for year 5, and so on). In short Farmer Lister has to figure out how to turn the infinite sum of
\[ 1 + \sum_{n=1}^{\infty} \frac{1}{3^n} \]
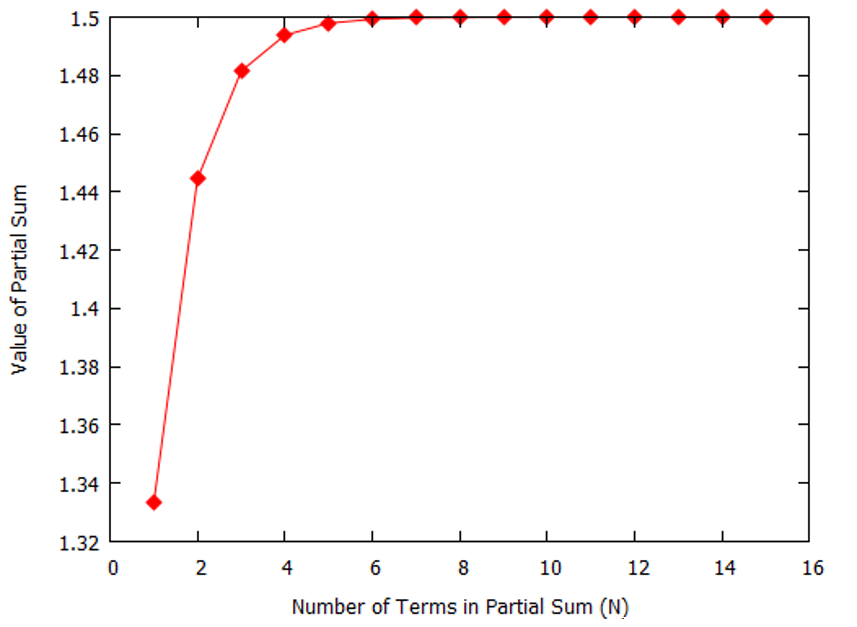
into something he can specify in terms of the goods manifest. Knowing some calculus, he tries graphing the partial sum as a function of $n$ and finds that the partial sums seem to quickly converge to the value of 1+1/2.
Encouraged by this result, he examines what happens if he takes 1+1/2 = 3/2 bushels. During the first year he plants 1+1/2 bushels and gets a final crop yield of 3 + 3/2 bushels. His family now has 3 bushels to eat and 1+1/2 bushels to plant. Thus the process is self-sustaining and he concludes that the infinite sum has a finite value
\[ \sum_{n=1}^{\infty} \frac{1}{3^n} = \frac{1}{2} \; . \]
It is worth noting that Farmer Lister was able to imagine crowing crops indefinitely, even though he can’t actually do that, and was able to have insight into how an infinite number of things combine to form something finite. This is the power of the human intellect and the magic of the process of growing food.