The last column introduced the basic structure of the propositional logic consisting of 10 inference rules that manipulated 5 logical symbols: negation $\neg$, conjunction (and) $\land$, disjunction (or) $\lor$, conditional $\rightarrow$, and biconditional $\leftrightarrow$.
The point of the system was to formalize the rules of reasoning so that two difficulties of natural language were eliminated. The first difficulty is that natural language premises (e.g. it is raining) are unwieldy compared to single symbols (e.g. R). The second, and more problematic, difficulty is the ambiguous aspect of natural language.
Suppose that a friend says “I am interested in logic and programming. Could you help me find good websites?” You try to help by doing a web search. How should you frame your search string? Does you friend mean that he is interested in getting hits that deal either with logic or with programming? Or perhaps he only wants sites that discuss both concepts in the same posting. With this ambiguity present, how should the search engine interpret the simple search string ‘logic programming’?
By formalizing and abstracting the objects and rules away from natural language, propositional calculus seeks a clean way of reasoning with algorithmic precision. The line of reasons that infers a set of well-formed formulas (wffs) from an initial set is called, appropriately enough, a proof. The flow of the proof is improved by abbreviating the rules of inference with a 2 or 3 character abbreviation:
- Modus ponens = MP
- Negation Elimination = $E\neg$
- Conjunction Introduction = $I\land$
- Conjunction Elimination = $E\land$
- Disjunction Introduction = $I\lor$
- Disjunction Elimination = $E\lor$
- Biconditional Introduction = $I\leftrightarrow$
- Biconditional Elimination = $E\leftrightarrow$
- Conditional Proof = CP
- Reductio ad Absurdum = RAA
I don’t find any proofs, except the most elementary ones, particularly easy to figure out and, I suppose, that is the point. If it was easy, there would be no need for the formalism.
As an example (taken from problem 3.31 of Theory and Problems of Logic by Nolt and Rohatyn), consider how to prove the following argument.
$ \neg( P \land Q) \rightarrow \neg P \lor \neg Q $
To recast that in natural language, let P stand for the sentence ‘it is raining’ and Q for ‘the streets are wet’. The argument above says that ‘if it is not true that it is raining and the streets are wet then either it is not raining or the streets are not wet’. This translation is not only a mouthful but, it may seem to some that it is also incomplete. In natural language, the ‘or’ in consequent can be interpreted as being an exclusive or – hat either it is not raining or that the streets are not wet but not both. However, the ‘or’ of propositional logic is the inclusive or that means the assumption is true if the first is true alone, the second is true alone, or both are true. Thus the propositional calculus arrived at a proof that, on the surface, may seem a surprise to the natural language ear.
The formal proof for this argument is given by:
The indentations denote hypothetical proofs within the main body of the proof (this one has 3 Reductio ad Absurdum sub-proofs) and the notation in the last column gives the line number(s) and the rule used to manipulate the wffs.
It is reasonable to ask why go through all this bother. Surely we don’t need formal logic to figure out if it is raining or if the streets are wet. There are several good reasons for studying the propositional calculus but perhaps the most interesting and important is that the system can be programmed on a computer and the rules of inference can be used on problems much harder than the human mind may be willing to deal with.
An interesting example of this is the Tree Proof Generator.
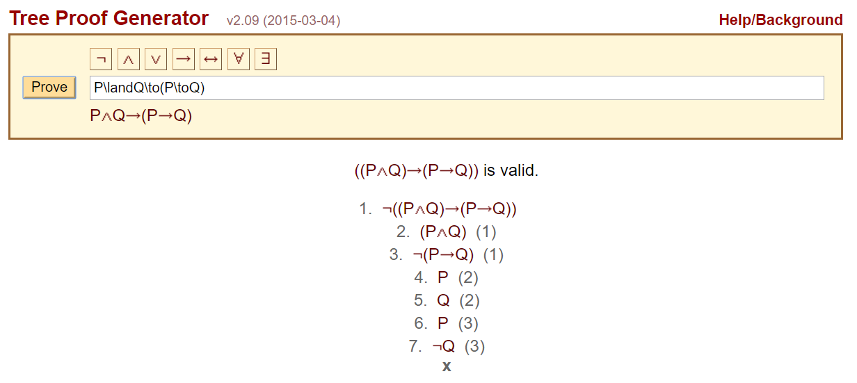
This web-based application allows the user to enter an argument its internal inference engine not only determines the arguments validity but it generates the step-by-step proof.
Now this example may not be particularly motivational until one stops to consider to the scope. Since the well-formed formula can be anything, such a system could solve complex mathematical problems, or go through complicated epidemiological analysis to assist in diagnosing a patient’s illness or in determining the pattern of a epidemic.
In other words, the propositional calculus can be used to make an expert system that can deal with large amounts of data and inferences in a formal way that would be difficult of impossible to people to do unaided.
Next week, I will look at what has been done with such expert agents – in particular with an agent application that attempts to keep a digital explorer from a gruesome cyber-fate.
