Something about the book ‘Five Golden Rules: Great Theories of 20th-Century Mathematics and Why They Matter’ by John L. Casti caught my eye the other day at the library. On a whim, I signed the book out and started reading. Living up to the promise of the title, the book had five chapters, each one devoted to one of the great math theories of 20th century. All in all, I had been exposed, at least superficially, to all the topics covered so I wasn’t sure what I would get out of the book other than some additional insight into material I already knew or confirmation of my wisdom in staying away from topics that I didn’t.
Anyway, I am quite glad that the mechanism of providence pointed me at this book because the connections that Casti draws are worth thinking about. None of these connections was as profound for me as the deep link that he explores in Chapter 4 entitled ‘The Halting Theorem (Theory of Computation)’.
In this chapter, Casti first presents the concept of the universal Turing machine (UTM) as a mechanism for attacking the question of Decision Problem (or Entscheidungsproblem) proposed by David Hilbert in 1928. Casti then couples this presentation with a discussion of the famous Gödel Incompleteness Theorem.
I’m simply a beginner in these fields and Casti omits important details and glosses over a variety of things to help the novice. From this point-of-view, I can’t recommend his work. But I am grateful and excited about the perspective he provided by making this linkage.
To understand my excitement, let me first try to fill in some of the background as best as I can.
Hilbert’s Decision Problem asks the following question. Given a set of input data and an algorithm for manipulating said data, is there a way to know if the algorithm will be able to make a yes/no decision about the input. For example, if the input data is a set of axioms in a logical system and some corresponding assertion in the same system and the algorithm is a logical formalism, such as the classical syllogism, will the algorithm be able to prove or disprove the assertion as either true (yes) or false (no)?
While the Decision Problem might seem straightforward enough to talk about it at a seminar, when it comes to actually tackling the question there are some vague conceptions that need further elaboration. Specifically, what does the term ‘algorithm’ really mean and what constitutes a workable algorithm seem to have been the murkiest part when the problem was first posed.
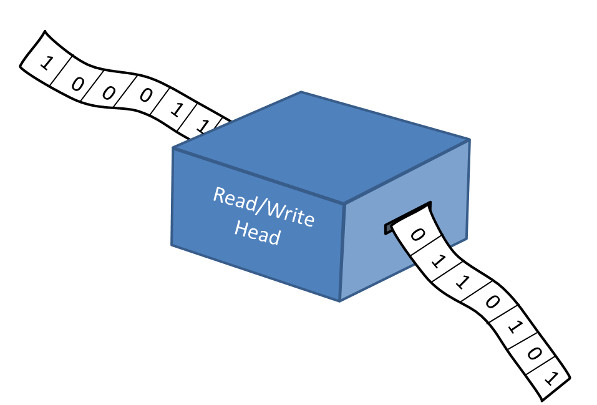
Turing chose to clarify the algorithm concept by the invention of the machine which bears his name. The UTM is a basic model of computation that is often used to understand the theory behind computer programming. It is also the avenue that allowed Turing to a way to tackle Hilbert’s Decision Problem. The basic ingredients for a UTM are a tape or strip of paper, divided into squares, a set of symbols (usually ‘0’ and ‘1’) that can be written into the squares, and a box that has a mechanism for moving the strip left or right, a head that reads from and writes to the strip and that contains an internal state that allows the UTM to select an action from a pre-defined set, given the internal state and current symbol being read. A typical graphical representation of an UTM looks like
The UTM can represent the input to the decision process by a particular pattern of symbols on the strip. It can also implement the step associated with an algorithm by encoding these also to symbols on the tape. So the entire nature of the Decision Problem comes down to the question as to whether once the UTM starts if it will ever halt; hence the name of the name of the chapter.
Kurt Gödel took a different approach to answering the Decision Problem. He developed a way to map any formal system to a set of numbers, called Gödel numbers. Then by formally manipulating these numbers, he was in position to try to answer Hilbert’s challenge.
Now it is reasonable to suppose that all not every question has a yes or no answer. Questions about feeling, opinion, or taste spring to mind. But I think that most of us expect that questions of mathematics and logic and programming have answers and that we should be able to figure them out. The remarkable thing about the work of both Turing and Gödel is that there are cases where the formal logical system simply can’t decide.
In the language of Turing, there are computational problems for which there is no knowing beforehand if the algorithm will terminate with an answer. In the language of Gödel, no matter is done to a logical system in terms of refining existing axioms or adopting new ones, there will always be truths that are unprovable.
I was quite aware of Godel’s theorem and even wrestled with it for a while when I was concerned about its implications to physical systems. Eventually, I decided that while man’s logic may be limited, nature didn’t need to worry about it because she could make decisions unencumbered by our shortcomings.
I was also quite aware that Turing’s machine was used fruitfully as a model computation. What I was unaware of until reading Casti’s book was the parallel between the conclusions of Gödel and of Turing.
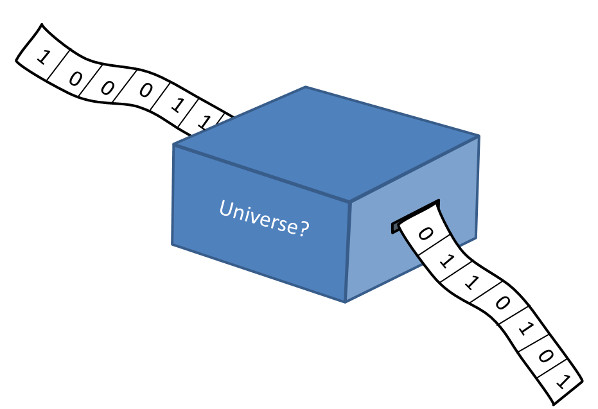
And here we arrive at the source of my excitement. As I’ve already said, I remain convinced that Nature can decide – that is to say that Nature is free of the issues discussed above. And yet, in some capacity the Universe is an enormous Turing machine.
So why does Nature always make a decision and why does the computation of trajectories, and the motion of waves, and evolution of quantum bit of stuff always reach a decision? It may not be the decision we expect or anticipate, but it seems clear that a decision is reached. And so, by looking at how the Universe as a Turing Machine (UaaTM) differs from a Universal Turing Machine, one may learn more about both. This is the exciting new idea that has occurred to me and one which I will be exploring in the coming months.