Up to this point, this series of blogs on computer algebra within SymPy have scraped the surface, looking at some of the basic problems that can arise and the primitive or atomic methods that can be used to manipulate certain pieces of an expression.  Hopefully, along the way, a new appreciation for the talents and faculties that even ordinary people have in recognizing patterns within the symbols of algebra has also been obtained.

Starting in this blog, we begin to dig much more deeply into the SymPy tree-structure and the syntactical rules that can be used to manipulate it.  These manipulations will be more structural and not mathematically semantic.  As an example of the distinction, we will be looking at ways to modify and rearrange the tree and its contents without ever asking if it is mathematically legitimate to do so.

There are three basic areas to develop a facility with:

1. Being able to detect if any two tree structures are the same
2. Being able to detect that a specified pattern exists within a larger tree
3. Being able to rewrite some portion of the tree.

When used together, we should be able to direct or guide the computer to rewrite expressions of arbitrary size into other expressions based on some prescribed specifications.  This type of direction or guidance should not be confused with automatic term rewriting such as encountered in a rule-based system.  In this latter case, deep questions about whether such automatic rewriting converges to a normal form (defined as the final, unchanging result) from repeated application of the rules arise and are quite difficult to settle.  Our aims are much more modest; we simply want a set of tools that can allow us to dictate what should be done in the rewriting without having to perform the individual steps by ourselves. 

In this blog post, we’ll explore the first basic step.  We’ll defer the other two steps to future blogs.

The first step in understanding the tree structures that underly an expression is to recognize that mathematically equivalent expressions need not result in the same tree structures.  This is a point quite distinct to the ‘special cases’ that arise when trying to work with exponentials or square roots.

The second step in understanding the tree structures is to also recognize that SymPy will sometimes mask the first rule by carrying out certain simplifications before constructing the final tree representation.

To illustrate these two points, let’s look at six sets of mathematically equivalent expressions: 1) Pure Addition, 2) Pure Multiplication, 3) Square of a Pure Expression, 4) Mixed Addition, 5) Mixed Multiplication, and 3) Square of a Mixed Expression.

Pure Addition

The first set of mathematically equivalent expressions deal with how addition of multiple terms are processed and represented:

\[ a + b + c + d = d + b + c + a = b + d + a + c = \ldots \; . \]

No matter which of the 24 possible permutations are entered, SymPy automatically sorts the input strings and provides the same tree structure.  For instance, $\text{expr1} = a + b + c + d$ gives the tree

and $\text{expr2} = d + b +c + a$ gives the same tree

In addition we can ask is the expressions associated with each are recognized by SymPy as being the same.  SymPy provides several ways to do this with the most convenient being the ‘==’ operator.  Thus

\[ \text{expr1} == \text{expr2} \; \]

yields True.

Pure Multiplication

In a similar way we can see that $\text{expr1} = a \cdot b \cdot c \cdot d$ and $\text{expr2} = d \cdot c \cdot a \cdot b$ yield the same tree

and that $\text{expr1} == \text{expr2}$ yields True.

Square of a Pure Expression

Our next example involves composing two separate functions.  The expressions are $\text{expr1} = (x+a)^2$ and $\text{expr2} = (a+x)^2$, both give the same tree,

and $\text{expr1} == \text{expr2}$ yields True.  Note that the presence of the Add results in another tier in the expression tree.

In all of these cases, SymPy produces the same expression tree because it sorts the input strings when the expressions are defined and the expressions are relatively simple.  Thus it is able to easily determine that these mathematically equivalent expressions are also structurally equivalent using ‘==’.

In the next set of mathematically equivalent expressions, we’ll find that SymPy’s ‘==’ operator will return True only sometimes and False in others.  This wrinkle will happen because the expression trees will get more complicated all because of the inclusion of a ‘-1’.

Mixed Addition

The first example involves changing the sign of one of the Symbols used in the Pure Addition case:

\[ a + b + c – d = -d + b + c + a = b – d + a + c = \ldots \; . \]

Of the 24 possibilities let’s let $\text{expr1} = a + b + c – d$ and $\text{expr2} = -d + b +c + a$.  Evaluating each of these gives the same tree

While SymPy does sort the symbols note that the ‘d’ is at a lower level with the SymPy function Mul occupying the same level that ‘d’ had in the previous version since the presence of a minus sign automatically creates a mixed tree that has more functions than Add.

Nonetheless, $\text{expr1} == \text{expr2}$ yields True since the two expressions are both mathematically and structurally equivalent.

Mixed Multiplication

In this next example, we let $\text{expr1} = -a \cdot b \cdot c \cdot d$ and $\text{expr2} = b \cdot a \cdot c \cdot (-d)$.  SymPy once again sorts the inputs and produces the same expression tree for each one:

Note that here, because $-a = -1 \cdot a $, the tree that results is only different in one single term – the addition of the NegativeOne symbol in the tree.  And, as expected, ‘==’ yields True when operating on both expressions.

Square of a Mixed Expression

The final set of mathematically equivalent expressions are

\[ (x-a)^2 = (a-x)^2 \; \; .\]

Regardless of the class of objects that $x$ and $a$ are (i.e., whole numbers, integers, real numbers, complex numbers, matrices, etc.) this identity holds since one can factor out a $-1$ from either side which squares to the identity:

\[ (a-x)^2 = ((-1)(x-a))^2 = (-1)^2 (x-a)^2 = (x-a)^2 \; .\]

However, the tree structure associated with each term is different.  The expression $\text{expr1} = (a-x)^2$ has the tree structure on the left while $\text{expr2} = (x-a)^2$ has the structure on the right.

Since the tree structures are different, $\text{expr1} == \text{expr2}$ yields False.  There is a way to demonstrate that they are mathematically equivalent by evaluating $\text{simplify( expr1 – expr2)}$ to zero.

Unfortunately, simplify isn’t a silver bullet.  First, since it throws a complex set of primitive simplification techniques at an expression following a heuristic it doesn’t allow us to find small differences in a tree structure (like that above) so it doesn’t help when we want to make a ‘surgical’ change.  SymPy’s simplification is like a sledge hammer in comparison.  In addition, it isn’t guaranteed to work.  So, we need to have ‘==’ in the toolbox.

This month, we will take a first look at ‘simplifying’ expressions and the some of the primary differences in how humans do it by hand versus how it is done when humans coax a machine to do it by manipulating a machine representation.

I’ve had occasion, when starting this series of blog posts, to reference Peter Norvig’s Paradigms of Artificial Intelligence Programming: Case Studies in Common LISP and I’ll do so again

Last month’s examination of the complexities associated with traversing the tree with the goal of factoring a subexpression, although the approach was optimal, illustrates some of the difficulties.  In fact, those difficulties are the tip of the iceberg for what is a subdiscipline in computer science that is called term rewriting. 

Term rewriting is a mathematically sophisticated and subtle subject and, for this installment at the least, we will confine ourselves to the built-in functions provided by SymPy for performing term rewriting that happens largely without direct involvement from the user and can be said to fall under the heading of simplification.  For the purposes of this discussion, simplification is defined as a method for generally making the number of terms in an expression go down and it should be held in contrast to expansion that generally makes the number of terms go up.

As an example, consider the tree expressions for the example Norvig provides.  The tree for $x^2 + 3x + 2$ looks like

with seven nodes.  The corresponding tree for $(x-1)(x-2)$ looks like

with 6 nodes.  So there is a savings in terms of tree representation even though there are more typographical symbols needed in rendering $(x – 1)(x – 2)$ (eight of them, ignoring whitespace) versus $x^2 + 3x + 2$ (seven of them, ignoring white space and the ‘^’ used to typeset the exponent).  The point of this somewhat whimsical discussion is that simplification is not only a matter of utility (what Norvig describes as ‘relative to what you want to use the expression for next’) but also of aesthetics. 

In any event, there are at least 11 specialized simplification methods in SymPy.  The following table lists them (with much of the verbiage taken from the help pages), their nominal purpose, and an example of each.

Each of the functions above are building blocks in working through the steps of term rewriting.  They represent common processes for specific steps.  However, they are incapable of performing all the steps needed to simplify a generic expression.  The generic function simplify “tries to apply intelligent heuristics to make the input expression “simpler”.”  It is interesting to note that again the machine is far more brittle and unintelligent than an average human.

In subsequent blog posts, we’ll explore subs, replace, and xreplace methods within SymPy.   These methods are the three ‘canonical’ methods within SymPy for rewriting terms that can be used in conjunction with the methods above to cover broader aspects of term rewriting.

Last month we started on a journey to explore and experiment with the computer algebra system SymPy that is freely available in the Python ecosystem.  The aim is to create, within this package, a rule system that implements the basic transformations and identities of the Fourier Transform.  But the goal is very loose and a great deal of emphasis is placed on the journey more so than the final product.  To this end, there are three focus areas:  1) working out the steps needed to manipulate symbolic expressions, 2) looking at what an intelligent agent would need to do as a way of exploring more artificial intelligence, and 3) discovering how the human does these steps differently and, in the process, having some new found appreciation for the subtleties and brilliance of the human mind.

To start, we look at a classic algebraic manipulation that comes up often in the study of all sorts of disciplines ranging from computer graphics, to gravity and electromagnetism, to geometry and trigonometry – namely the application of the Pythagorean theorem to find the distance or magnitude of a vector by computing the square root of the sum of the squares.

To keep things notationally simple, we’ll consider the very simple expression:

\[ D = \sqrt{ (x-a)^2 + y^2 } \; \]

made up of the symbols $\{a,x,y\}$.

In a variety of settings, society ‘expects’ that competent students of algebra to either recognize or, at a minimum, be able to verify that

\[ D’ = \sqrt{ x^2 – 2 a x + a^2 + y^2} \; \]

is ‘equal’ to $D$. 

Of course, the word ‘equal’ very elastic and, as a result, it isn’t precise enough for either deep exploration of the human mind or for the shallow, do-as-I-am-told workings for a computer.  Let’s try to nail that down with some better definitions.

First, let’s define the term mathematically equal to contain the meaning that a teacher wants to convey when he says that $D=D’$.  Mathematical equality means that for every choice of values for $\{a,x,y\}$ the numerical result obtained by substitution from $D$ is exactly the same as the numerical result obtained from $D’$ by the same process.

Now let’s define the term structurally equal to mean that the formal way the symbols are written in the expression are the same even if the identity of the symbols are not.  For example,

\[ D’’ = \sqrt{ (q-q_0)^2 + p^2 } \; \]

is structurally equal to the expression for $D$ since we recognize that the symbol substitutions

\[ x \rightarrow q \; ,\]

\[ a \rightarrow q_0 \; , \]

and

\[ y \rightarrow p \; \]

make $D$ look the same on paper as $D’’$.  Note that two expressions that are structurally equal need not be mathematically equal if assumptions about the different symbols aren’t the same.  For example, if $x \in (-\infty,\infty)$ but we restrict $p \in [0,\infty]$, then, despite their structurally equality $D$ is not mathematically equal to $D’’$ when $x < 0$.

We will use the term exactly equal to mean that two expressions are both mathematical equal and structurally equal and have the same symbols.

These three definitions have holes and limitations.  The holes are a by-product of limitations of human logic and we won’t try to patch them so much as work around them when the time comes.  Regarding the limitations, we can give a general notion of where they will show up and then revisit them in the future.  The primary limitation(s) is that the notion of equivalency is left out.  To give a flavor of this consider the two expressions

\[ \frac{d}{dx} \left( x^2 – 3 a x + 9 \right) \; \]

and

\[  2x -3a \; .\]

These two expressions are neither mathematically equal (one can’t simply substitute in a value for $x$ before taking the derivative) nor structurally equal (the symbol structure isn’t the same).  But they are equivalent in the sense that applying the derivative in the first leads one to the second.  And, there is another wrinkle when considering moving from the second expression to the first, in that $2x – 3a$ is equivalent to an infinite number of expressions of the form

\[ \frac{d}{dx} \left( x^2 – 3 a x + constant \right) \; .\]

Since we will have our hand full just dealing with how to teach an agent how to determine if $D$ is structurally or mathematically equal to $D’$, we will defer these deeper matters and look at a simple example from basic physics.

It is typical for a professor, when teaching say electromagnetism, to look at $D’$ and simply highlight the first three terms under the radical and say something to the effect that the form a perfect square which can be ‘reduced’ or ‘simplified’ to the other.

However, there is no cognitive mind behind a computer (no matter how much training data it may have ingested) and so it can’t fill in the gaps and move (albeit not usually effortlessly) between the various ambiguities and elastic meanings in the way a human can. 

To understand this point better, consider that to represent the expression above requires nesting $x^2 – 2 a x + a^2 + y^2$ under a square root symbol.  That’s four terms ‘owned’ by the square root, which we wish to ‘factor’ into two terms $(x-a)^2 + y^2$.  In addition, each of these terms is complicated as none are ‘atomic’.  A term is atomic if it consists of a symbol and nothing else.

Driving this point home is easier done with a visual. Using the graphviz application and the corresponding Python API, we can visually display how these various expressions are represented internally.  SymPy uses a tree structure that, for the expression $D’$, looks like

Every node in the a SymPy tree is either a function or a symbol.  Functions own (almost always) children nodes reflecting their composite.  Symbols are terminal nodes reflecting their atomic nature.  At the top of the tree is the Pow function (for power) with two main branches:  Add and Half.  Add is the function that owns the four terms that algebraically add together while Half is a special symbol meaning 1/2.  SymPy reserves a special symbol for this since division by 2 is so common.  Of the four main branches of Add, three are Pow and one is Mul (for multiply).  Like Add, Mul can own an arbitrary number of branches.  In this case there are three, each terminating with the symbols $-2$, $a$, and $x$.  

In order to manipulate the only some of the contents under the square root we must be able to find that portion of the tree that corresponds to $x^2 – 2 a x + a^2$, remove it, manipulate it, and then return the new structure to the tree so that it looks like:

Getting the contents of the square root is relatively simple:  we simple ask for the arguments of the expression and we get a tuple containing the Add branch and the Half Symbol.

The Add branch is now a polynomial expression that we might be tempted to try SymPy’s factor on.  However, Factor doesn’t know what to do with the portion involving $y^2$.  However, if we isolate the portion of the expression involving just $x$ and $a$ by subtracting off the $y^2$ piece, factoring, and then adding $y^2$ back, we get a reasonable result.  Both of these approaches are shone in the notebook snippet below:

This behavior is not unique to either this situation nor to SymPy.  Asking Wolfram Alpha to factor $x^2 -2 a x + a^2$ works fine but asking it to perform the same function on $x^2 -2ax + a^2 + y^2$ doesn’t give an acceptable answer (although its answer differs from SymPy’s default but coincides with SymPy being directed to factor of the field of the reals).

Two final points.  First, there is an algorithmic way of doing the separation of the polynomial into a $a$-$x$ part and a remainder that can be run without as much hand-holding as this snippet shows:

a, x, y = sym.symbols(‘a x y')

poly = x**2 - 2*a*x + a**2 + y**2

ax_part = sum(
    term for term in expr.as_ordered_terms()
    if term.has(a, x) and not term.has(y)
)

rest = poly - ax_part

sym.factor(ax_part) + rest

Second, and far more important.  Just for fun, I asked Chat GPT to factor $x^2 -2 a x + a^2 + y^2$ both absent from and under the square root and it delivered the ‘professorial’ answer $(x-a)^2 + y^2$ in either case.  It was also able to factor a more difficult SymPy example of $2x^5 + 2x^4y + 4x^3 + 4x^2y + 2x + 2y + a$ into $2(x+y)(x^2 + 1)^2 + a$ even though both Wolfram Alpha and Sympy could not out of the box.  I suspect the reasons for these successes are either that these are well-known examples that reside somewhere within its system or it knows how to make these systems work better than I do.  The next logical question is then why are SymPy and Mathematica not out of business.  I think the only answer to this is that these success are superficial.  That real mathematical creativity is still beyond the capabilities of the machine.  But, I suppose, time will tell.

One of the most active areas of artificial intelligence in the earlier days (say from 1960s through the 1990s) was the development of symbolic AI to handle mathematical manipulations.  In his book, Paradigms of Artificial Intelligence Programming: Case Studies in Common Lisp, Peter Norvig covers numerous applications that were solved as the ‘hot’ topics of the day; a time before the before the advent of deep learning came along and convinced most people that LLM’s and agentic systems would solve all the world’s problems.  However, these former hot topics are still relevant today and I thought that it might be interesting to explore a bit to see what can be done with ‘old fashioned’ symbolic manipulation.

There are three reasons for embarking on this exploration. 

First, understanding the nuts and bolts of symbolic manipulation makes one a better user of the ‘professional’ computer algebra systems (CASs) on the market today, such as wxMaxima, Maple, Mathematica, and SymPy.  Each of these is polished and abstracted (to varying degrees) and seeks to help the user, typically a mathematician, scientist, or engineer, in making a model and subsequently applying it to some specific problem.  However, each of these systems (especially the for-profit ones), want the user to be able to solve problems immediately without, necessarily, knowing how the CAS works behind the scenes.  While these systems are quite powerful (again to lesser or greater degrees), experience has shown that most users don’t/can’t take full advantage of the system unless they can program in it.  And to program in it requires a firm understanding of at least the rudiments of what is happening under the hood.  This is a sentiment Norvig emphases repeatedly in his book, most notably by providing the following quote:

Second, there are always new mathematics being invented with brand new rules.  Being able to manipulate/simplify and then mine an expression for meaning transcends blindly applying a built-in trig rule like $\cos^2 + \sin^2 = 1$, a generic ‘simplify’ method, or some such thing.  It often requires understanding how an expression is formed and what techniques can be used to take an expression apart and reassemble as something more useful.

Third, and finally, it’s fun – plain and simple – and most likely will be a gateway activity for even more fun to come.

Not that we’ve resolved to explore, the next choice is which part of terra incognita.  The undiscovered country that I’ve chosen is the implementation of a simple set of symbolic rules, via pattern matching, that implement some of the basic properties of the Fourier Transform.

For this first experiment, I chose Sympy as the tool of choice as it seemed a natural one since it provides the basic machinery of symbolic manipulation for free in Python but it doesn’t have a particularly sophisticated set of rules associated with the Fourier Transform.  For example, SymPy version 1.14 knows that the transform is linear but it doesn’t know how to simplify the Fourier Transform based on the well-known rule:

\[ {\mathcal F}\left[ \frac{\partial f(t)}{\partial t} \right] = i \omega {\mathcal F}\left[ f(t) \right] \; , \]

which is one of the most important relationships for the Fourier Transform as it allows us to convert differential equations into algebraic ones, which is one of the primary motivations for employing it (or any other integral transform for that matter).

Before beginning, let’s set some notation.  Functions in the time domain will be denoted by lower case Latin letters (e.g., $f$, $g$, etc.) and will depend on the variable $t$.  The corresponding Fourier Transform will be denoted by upper case Latin letters (e.g., $F$, $G$, etc.) and will depend on the variable $\omega$.  Arbitrary constants will also be denoted by lower case Latin letters but usually from the beginning of the alphabet (e.g., $a$, $b$, etc.). The pairing between the two will be symbolically written as:

\[ F(\omega) = {\mathcal F}(f(t)) \; ,\]

with an analogous expression for the inverse.  The sign convention will be chosen so that the relationship for the transform of the derivative is as given above.

For the first experiment, I chose the following four rules/properties of the Fourier Transform:

1. Linearity:  ${\mathcal F}(a \cdot f(t) + b \cdot g(t) ) = a F(\omega) + b G(\omega)$
2. Differentiation: $\mathcal{F}\left[\frac{d^n f(t)}{dt^n}\right] = (i \omega)^n F(\omega)$
3. Time Shifting:  $\mathcal{F}{f(t – t_0)} = e^{-i \omega t_0} F(\omega)$
4. Frequency Shifting: $\mathcal{F}{e^{i \omega_0 t} f(t)} = F(\omega – \omega_0)$

We expect freshman or, at worst, sophomores in college to absorb and apply the rules above and, so, we may be inclined to think that they are ‘straightforward’ or ‘boring’ or ‘dull’.  But, finding a way to make a computer do algorithmically what we expect teenagers to pick up from a brief lecture and context is surprisingly involved. 

Our hypothetical college student’s capacity to learn, even when not explicitly taught is an amazing and often overlooked miracle of the human animal.  Unfortunately, teaching any computer to parse ‘glyphs on a page’ in a way that mimics what a person does requires a lot of introspection into just how the symbols are being interpreted.  Mathematical expressions are slightly easier as they tend to have less ‘analogical elasticity’; that is to say, that by their very nature, mathematical terms and symbols tend to be more rigid that everyday speech.  More rigid doesn’t mean completely free of ambiguities as the reader may reflect on when thinking about what the derivatives in the Euler-Lagrange equations actually mean:

\[ \frac{d}{dt} \left( \frac{\partial L}{\partial {\dot q}} \right) – \frac{\partial L}{\partial q} = 0 \; . \]

Let’s start with a simple mathematical expression that is needed for the Linearity property

\[ a \cdot f(t) +  b \cdot g(t) \; . \]

When composing this expression, a person dips into the standard glyphs of the English alphabet (10 of them to be precise) and simply writes them down.  If pressed, the person may go onto say “where $a$ and $b$ are constants and $f$ and $g$ are, as yet undefined functions of the time variable $t$”.  But the glyphs on the page remain all the same.  For a computer, are the glyphs ‘a’ and ‘b’ of the same type as the glyphs ‘f’ and ‘g’?  And where does ‘(t)’ figure in? 

SymPy’s answer to this (which matches most of the other CASs) is that ‘a’, ‘b’, and ‘t’ are Symbols and ‘f’ and ‘g’ are undefined Functions.  The bold-face terms are syntactically how SymPy creates these symbolic objects. These objects can be used as ordinary Python objects with all the normal Python syntax (e.g., print(), len(), type(), etc.) coming along because SymPy tries to strictly adhere to the Python data model.  As a result, we can form new expressions by using ‘+’ and ‘*’ without worrying about how SymPy chooses to add and multiply it various objects together.

The following figure shows the output of a Jupyter notebook that implements these simple steps.

As expected, querying type(a) gives back sympy.core.symbol.Symbol and type(f) returns sympy.core.function.UndefinedFunction.  And, as expected, we can form our first expression

from using ‘+’ and ‘*’ as effortlessly as we wrote the analogous expression above out of basic glyphs, without having to worry about details.  But what to make of type(my_expr) returning sympy.core.add.Add?

The answer to this question gets at the heart of how most (if not all) CASs work.  What we humans take for granted as a simple expression $a \cdot f(t) + b \cdot g(t)$ is, for SymPy (and all the other CASs that I’ve seen), a tree.  The top node is this case is Add meaning that ‘+’ is the root and each of the two subexpressions ($a \cdot f(t)$ and $b \cdot g(t)$) are child nodes, each of type sympy.core.mul.Mul.  SymPy symbols are atomic nodes that can only be root nodes or child nodes but can never serve as parent nodes.  And the distinction between the Symbol and Function objects are now much clearer: giving a glyph the designation as a Function means it can serve as a parent node, even if all of its behavior is, as yet, undefined.

The innocent-looking expression from above has the tree-form

Next month, we’ll continue on to show how to examine, traverse, and modify this tree structure so that we can mimic how a human ‘plays with’ and ‘mine meaning from’ an expression.

The last post introduced the notion of the recursive least squares estimation approach as a natural precursor to the Kalman filter and derived the Kalman-like gain that governed the state estimation update equation.  Before moving on to a simple example of the Kalman filter, it seemed prudent to show the recursive least squares filter in action with a numerical example.

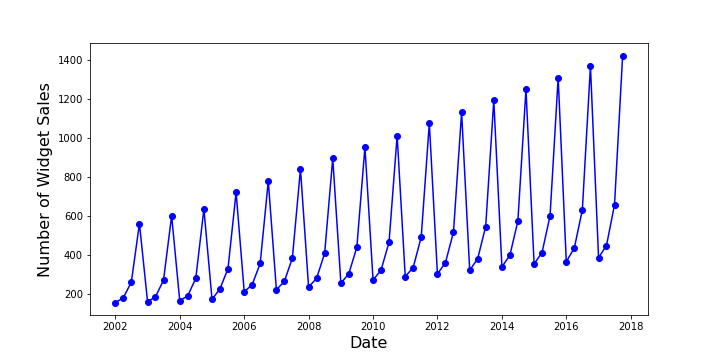
The example involves a mass falling in an unknown uniform gravitational field with unknown initial conditions.  At regular time intervals, a measurement device measures the height of the mass above the ground but only to within certain precision due to inherent noise in it measuring processes.  The challenge is then to deliver the best estimate of the unknowns (initial height, initial speed, and the uniform gravitational acceleration).   We will assume that, beyond a measurement of the initial height, the other initial conditions are inaccessible to the measurement device since it only measures range.  This example is adapted from the excellent article Introduction to Kalman Filter: Derivation of the Recursive Least Squares Method by Aleksander Haber.

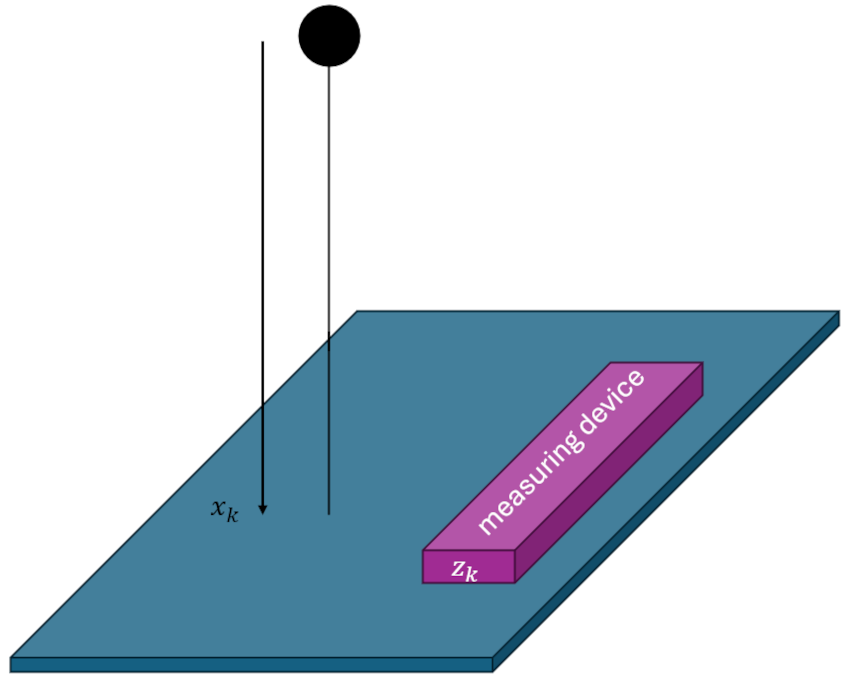
To prove that the recursive least squares method does generate a real least squares estimation, let’s first look at how a batch least squares approach to this problem would be performed.

The dynamics of the falling mass are given by

\[ d(t) = d_0 + v_0 t + \frac{1}{2} a t^2 \; , \]

where $d(t)$ is the height above the ground at a given instant.

We assume that the above equation is exact; in other words, there are no unknown forces in the problem.  In the language of Kalman-filtering and related optimal estimation, there is said to be no process noise, with it understood that the word ‘process’ is a genetic umbrella meaning the dynamics by which the state evolves in time, for which Newton’s laws are an important subset.

By design, measurements come in every $\Delta t$ seconds and so the time evolution of the fall of the mass is sampled at times $t_k = k \Delta t$.  At measurement time $t_k$ the amount the mass has dropped is

\[ x_k = x_0 + v_0 k \Delta t + \frac{1}{2} k^2 \Delta t^2  a \; \]

and the corresponding measurement is

\[ z_k = x_k + \eta_k \; , \]

where $\eta_k$ is the noise the measuring device introduces in performing its job.

The batch least squares estimation begins by writing the evolution equation in a matrix form

\[ z_k = \left[ \begin{array}{ccc} 1 & k \Delta t & \frac{1}{2} k^2 \Delta t^2 \end{array} \right] \left[ \begin{array}{c} x_0 \\ v_0 \\ a \end{array} \right]  + \eta_k \equiv H_{k,p} x_p + \eta_k \; .  \]

The array $x_p$ contains the constant initial conditions and unknown acceleration that is being estimated.

For this numerical experiment, $x_0 = -4m$, $v_0 = 2 m/s$ (positive being downward), and $a = 9.8 m/s^2$ the usual value for surface of the Earth (give or take regional variations).  Measurements are taken every $\Delta t = 1/150 s$ over a time span of 14.2 seconds.  To illustrate the meaning of $H_{k,p}$, the value of the matrix at $k=0$ is

\[ H_{k=0,p} = \left[ \begin{array}{ccc} 1 & 0 & 0 \end{array} \right] \; \]

corresponding to an elapsed time of $t_k = 0$ and at $k = 75$

\[ H_{k=0,p} = \left[ \begin{array}{ccc} 1 & 0.5 & 0.125 \end{array} \right] \; \]

corresponding to an elapsed time of $t_k = 0.5$. 

The merit of this matrix approach is that by putting every measurement into a batch we can write the entire measured dynamics in a single equation as:

\[ z = H x + \eta \; . \]

The array $z$ has $M$ elements (for the number of measurement), where $M$ is the maximum value of the time index $k$ (for this specific example $M$ = 2131).  The matrix $H$ is a $M \times n$ where $n$ is the number of estimate parameters ($n$ = 3, in this case) and $x$ is the array of parameters to be estimated).  The array $\eta$ represents the $M$ values of random noise (assumed to be stationary) that were present in the measurements.  The values of $\eta$ used in this numerical example were drawn from a normal distribution with a zero mean and a standard deviation of 1; the latter value determines the value of $R_k = 1$.

Since, in the matrix equation above, the matrix $H$ isn’t square, it may not be obvious how to solve for $x$.  However, there is a well-known technique using what is known as the Moore-Penrose pseudoinverse. 

In short, to solve for $x$ in a least squares sense, we set $\eta$ to zero (i.e., we ignore the noise assuming the classical argument that with enough measurements the influence of the noise will average to zero).  We then left-multiply by the transpose of $H$ to get

\[ H^T z = (H^T H) x \; .\]

The quantity $H^T H$ is a $(n \times K) \cdot (K \times n) = n \times n $ matrix (in this case $3\times 3$, which is invertible.  We then arrive at the compact form of the estimate for $x$ as

\[ x_{est} = (H^T H)^{-1} H^T z \; .\]

For this numerical experiment, the resulting estimate is

\[ x_{est} = \left[ \begin{array}{c} -3.95187658 \\ 1.99300377 \\ 9.80040125  \end{array}    \right] \; .\]

This is the same value one gets by using a package like numpy’s linalg.lstsq.

In the recursive method, all of the data are not stored and handled at once but rather each point is taken and processed as it comes in. 

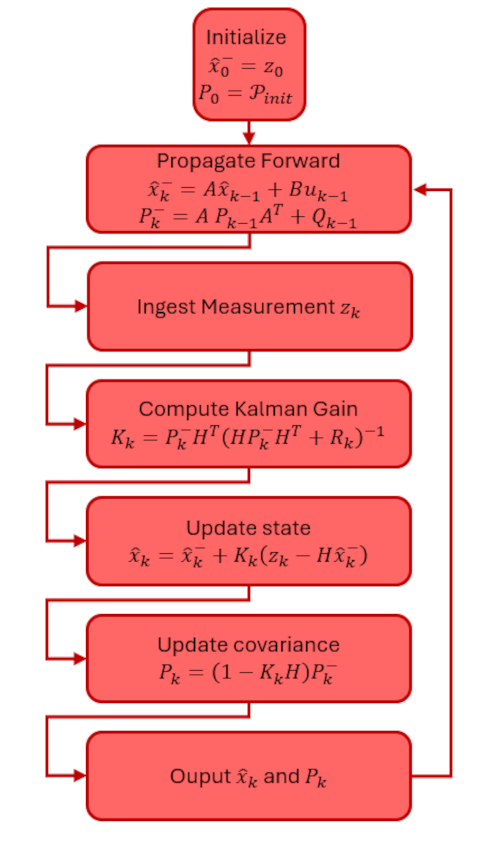
The algorithm developed in the last post is summarized as:

• Start each step with the current time $t_k$, measurement $z_k$, and the previous estimates of the state $x_{k-1}$ and the covariance $P_{k-1}$
• Perform the $k$-th calculation of the gain: $K_k = P_{k-1} \cdot H_k^T \cdot S_k^{-1}$, where $S_k = H_k \cdot P_{k-1} \cdot H_k^T + R_k$
• Make the $k$-th estimate of the unknowns: ${\hat x}_k = {\hat x}_{k-1} + K_k \left( z_k – H_k {\hat x}_{k-1} \right)$
• Make the $k$-th update of the covariance matrix: $P_k = \left(I – K_k H_k \right)P_{k-1} $

Using this algorithm, the time evolution of the estimated initial position is

with a final value of -3.95170034.

Likewise, the time evolution of the estimated initial speed is

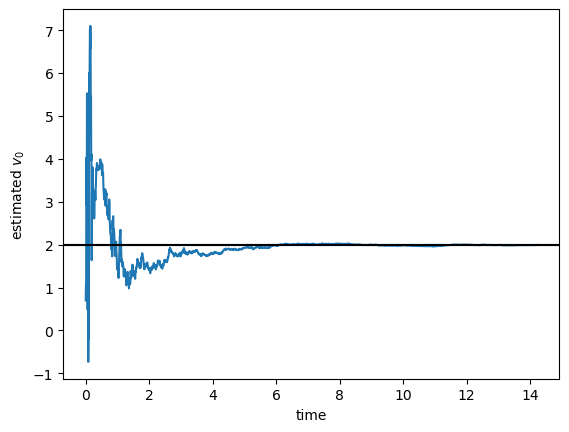
with a final value of 1.99295453.

And, finally, the time evolution of the estimated acceleration is

with a final value of 9.80040698.

These estimated values, up to the numerical noise introduced by a different set of floating point operations, are identical with the batch least squares numbers.

Last month’s blog presented one of the most common approaches to handling time series data in real time known as the Kalman gain.  As noted, the form of the state update equations is formally

\[ x_{new} = x_{old} + K ( obs_{new} – obs_{pred} ) \; , \]

where $x$ is the state being estimated and $obs$ is some observation made of the state.  The subscripts on the observation terms are ‘new’ for the latest actual observation (made by some instrument) and ‘pred’ for what the expected predicted observation would be before we made it. 

For the sequential or running average discussed in the first of these series of posts, this general form specifies as

\[ {\bar x} = {\bar x}^{-} + \frac{1}{N} \left( x_N – {\bar x}^{-} \right) \; , \]

where ${\bar x}$ is the estimated average.  For exponential smoothing (and, by extension Holt-Winter), discussed in the third of these series of posts, the general form becomes

\[ s_k = s_{k-1} + \alpha \left( x_k – s_{k-1} \right) \; , \]

where $s_k$ is the smoothed form of some time-varying quantity $x_k$.  For Kalman filtering, discussed in the fourth of these series of posts, the general form takes on the appearance of

\[ {\hat x}_k = {\hat x}_k^{-} + K_k \left( z_k – H {\hat x}_k^{-} \right) \; , \]

where ${\hat x}_k$ is the revised estimated state at time $t_k$ based on the difference between the current measurement $z_k$ and the a priori estimated state ${\hat x}_k^{-}$ at the same time. 

The ‘magic’ in all these cases lies firmly in determining the ‘gain’ that sits outside the difference between the new observation datum and the expected value of the same based on the previous estimate. 

In running average and Holt-Winter cases, it is fairly easy to deduce the form of the gain without any formal mathematical manipulations.  A few rearrangements and some intuition serve.  In the case of the Kalman filter a lot more effort is involved.

As a stepping-stone exercise which has almost all of the ingredients found in the Kalman filter but is both easier to understand and slightly easier to manipulate is the recursive least squares estimator.  The presentation below is strongly influenced by the excellent article Introduction to Kalman Filter: Derivation of the Recursive Least Squares Method by Aleksander Haber with mathematical simplifications gleaned from the Wikipedia entry on the Kalman Filter. 

Haber’s system of equations models a process in which a constant set of parameters are unknown but can be estimated from a time series of measurements of a time-varying state whose evolution is solely determined by the set of parameters.  The measurement equation is given by

\[ z_k = H_k x + v_k \; . \]

The time varying matrix $H_k$ serves to map the constant but unknown state $x$ forward in time.  The term $v_k$ represents the measurement noise, which is assumed to be zero-mean Gaussian distributed with a covariance given by

\[ E[v_k v_k^T ] = R \; .\]

The concrete example that Haber provides is an object being subjected to constant acceleration starting from an unknown initial position and speed.  The object’s motion obeys

\[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 =  \left[ \begin{array}{ccc} 1 & t & \frac{1}{2} t^2 \end{array} \right] \left[ \begin{array}{c} x_0 \\ v_0 \\ a \end{array} \right]  \equiv H(t) x \; .\]

The conversion from the continuous process matrix $H(t)$ to the discrete time-sampled $H_k$ is trivially done by noting that the time $t_k = k \Delta t$. 

Haber claims that a least squares estimation of $x$ can be determined recursively by the process

\[ x_k = x_{k-1} + K_k ( z_k – H_k x_{k-1} ) \; , \]

where $x_k$ is the current estimate of $x$, $z_k$ is the current measurement, and in which the gain $K_k$ will be given by the optimality condition that we want to minimize the error.

To find the explicit form of the gain, we first define the error in state estimation as

\[ \epsilon_k = x – {\hat x}_k \; . \]

Since the parameter set is generically multi-dimensional we will want to minimize the total error

\[ W = E[(\epsilon_k)_1^2] + E[(\epsilon_k)_2^2]+ \ldots + E[(\epsilon_k)_i^2] \; , \]

where the expectation is over all possible realizations of the random error in the measurement.  If we form the covariance matrix of the error

\[ P_k = E[ \epsilon_k \epsilon_k^T] \; \]

then the total error is trace of the covariance matrix: $W = Tr(P)$.  Taking the derivative of this trace and setting it equal to zero provides the explicit form for the gain as follows.

First, re-express the current estimation error in terms of the previous time estimation and via the update equation

\[ \epsilon_k = x – x_{k-1} – K_k(z_k – H_k x_{k-1}) \;  .\]

Using the measurement equation, current estimation error becomes

\[ \epsilon_k = x – x_{k-1} – K_k( H_k x + v_k – H_k x_{k-1} ) \; .\]

This last form re-emphasizes that, in the absence of the measurement noise $v_k$, the determination of the unknown parameter set $x$ would be exact since all the quantity in the parentheses would be identically zero.

Regrouping the terms so that the state variables are gathered separately from the noise yields

\[ \epsilon_k = (1 – K_k H_k) (x – x_{k-1}) – K_k v_k \equiv T_k (x – x_{k-1}) – K_k v_k \; . \]

Now it relatively easy to right multiply the above expression by its transpose

\[ \epsilon_k \epsilon_k^T = T_k (x – x_{k-1} ) (x – x_{k-1} )^T T_k^T + K_k v_k v_k^T K_k^T \\ – K_k v_K (x – x_{k-1} )^T T_k^T – T_k (x – x_{k-1} ) v_k^T K_k^T \; \]

and take an expectation of it to arrive at the covariance matrix

\[P_k = E[ (T_k (x – x_{k-1}) (x – x_{k-1})^T T_k^T]  – E[K_k v_k v_k ^T K_k^T] \; . \]

The cross-terms between the state and the measurement noise vanish under the assumption that the noise is zero-mean distributed (i.e., unbiased). 

Since $K_k$ and $H_k$ only depend on the time-independent value of the noise covariance $R$, they can be factored out of the expectation and we arrive at

\[ P_k = (1 – K_k H_k) P_{k-1} (1 – K_k H_k)^T + K_k R K_k^T \; , \]

which is the Joseph form of covariance propagation relating the covariance matrix at time $t_k$ to one at an earlier time $t_{k-1}$.

The last step is to take the trace and minimize it.  While there are a number of formulae for doing this step that engineers and mathematicians favor, it is easier to use index notation since it frees one from the bother of finding the correct formula and then applying it.

To proceed, expand the Joseph form term-by-term and define $S_k = H_k P_{k-1} H_k^T + R$, to get

\[ P_k = P_{k-1} – K_k H_k P_{k-1} – P_{k-1} H_k^T K_k^T + K_k S_k K_k^T \; . \]

Now, we can suppress the indices on the right since we know that every matrix bears a $k$ subscript except any covariance matrix, which must have a $k-1$ subscript.

The trace is then given by

\[ Tr(P_k) = P_{ii} – K_{ij} H_{j\ell} P_{\ell i} – P_{ij} C_{j\ell}^T K_{\ell i}^T + K_{ij} S_{j \ell} K_{\ell i} \; .\]

The least squares minimization is expressed as

\[ \frac{\partial Tr(P_k)}{\partial K_{st}} = 0 \; . \]

The derivative on the left can be expressed as

\[ \frac{\partial Tr(P_k)}{\partial K_{st}} = – H_{t \ell} P_{\ell s} – P_{sj}H_{jt}^T + S_{t \ell} K_{\ell s}^T + K_{sj} S_{jt} \; .\]

Re-arranging the terms and indices (subject to the transposes) to return to a matrix-multiplication form, yields

\[ \frac{\partial Tr(P_k)}{\partial K} = – 2 P_{k-1} H_k^T + K_k (S_k + S_k^T) \; , \]

where the $k$ index has been restored once the matrix indices have been suppressed.

The last step is to recognize that

\[ S^T = (H P H + R)^T = (H^T)^T P^T H^T + R^T = H P H^T + R \; \]

since both the state and noise covariance matrices are symmetric.

The final step is to set all of that equal to zero and solve to $K_k$.  Doing so gives

\[ K_k S_k = P_{k-1} H_k^T \; , \]

which immediately solves to

\[ K_k = P_{k-1} H_k^T S_k^{-1} = P_{k-1} H_k^T \left[ H_k P_{k-1} H_k^T + R \right]^{-1} \; .\]

Next blog, we’ll explore a numerical example of this method and establish that it does deliver the least squares estimation of the parameter set $x$.

This month we turn from the exponential smoothing and moving average techniques for analyzing time series and start a sustained look at the Kalman filter.  The Kalman filter has been hailed as one of the most significant mathematical algorithms of the 20^th century.  The primary reason for this praise is that the Kalman filtering enables a real time agent to make mathematically precise and supported estimates of some quantity as each data point comes in rather than having to wait until all the data have been collected.  This enabling behavior garners Kalman filtering a lot of attention and Russell and Norvig devote part of their chapter on probabilistic reasoning in their textbook Artificial Intelligence: A Modern Approach to it.

Before diving into the mathematical details, it is worth noting that the thing that sets the Kalman filter apart from the Holt-Winters algorithm is that in the latter, we needed to recognize and characterize a reoccurring pattern in our data.  For example, in the Red Fin housing sales, the data are conveniently regularly spaced in monthly intervals and seasonal patterns are readily apparent if not always predictable.  The Kalman filter imposes no such requirements, hence its usefulness.  It is often used in navigation activities within the aerospace field where it is applied to powered flight of a missile as readily as to a low-Earth orbiting spacecraft like Starlink to a libration orbiting spacecraft like JWST.

There are an enormous number of introductions to the Kalman filter each of them with their own specific strengths and weakness.  I tend to draw on two works: An Introduction to the Kalman Filter by Greg Welch and Gary Bishop and Poor Man’s Explanation of Kalman Filtering or How I stopped Worrying and Learned to Love Matrix Inversion by Roger M. du Plessis.  The latter work is particularly difficult to come by, but I’ve had it around for decades.  That said, I also draw on a variety of other references which will be noted when used.

I suppose there are four core mathematical concepts in the Kalman filter:  1) the state of the system can be represented by a list of physically meaningful quantities, 2) these quantities vary or evolve in time in some mathematically describable way, 3) some combination (often nonlinear) of the state variables may be measured, 4) the state variables and the measurements of them are ‘noisy’.

Welch and Bishop describe these four mathematical concepts as follows.  The state, which is described by a $n$-dimensional, real array of variables

\[ x \in \mathbb{R}^n \; \]

evolves according to the linear stochastic differential equation

\[ x_k = A x_{k-1} + B u_{k-1} + w_{k-1} \; , \]

where $A$, which is known as the $n \times n$ real-valued process matrix, provides the natural time evolution of the state at earlier time $t = k-1$ to the state at time $t = k$.  The quantity $u \in \mathbb{R}^{\ell} $ is a control or forcing term that is absent in the natural dynamics but can be impose externally on the system.  The $n \times \ell$, real-valued matrix $B$ maps the controls into the state evolution.  The term $w \in \mathbb{R}^n$ is the noise in the dynamics; it typically represents those parts of the natural evolution or of the control that are either not easily modeled or are unknown.

Measurement of the state is represented an $m$-dimensional, real-valued vector $z \in \mathbb{R}^m$ and is related to the state by the equation

\[ z_k = H x_k + v_k \; , \]

where $H$ is a $m \times n$ real-valued matrix and $v \in \mathbb{R}^m$ is the noise in the measurement.

In addition, both noise terms are assumed to be normally distributed with their probabilities described by

\[ p(w_k)  = N(0,Q_k) \; \]

and

\[ p(v_k) = N(0,R_k) \; , \]

where $Q_k \in \mathbb{R}^{n \times n}$ is the process noise covariance matrix and $R_k \in \mathbb{R}^{m \times m}$ is the measurement noise covariance matrix.  We further assume that they are uncorrelated with each other.  Generally, these noise covariances are time-varying since their values typically depend on the state.

Note that both the state and measurement equations are linear.  More often than not, Kalman filtering is applied to nonlinear systems but in those cases, the estimation process is linearized and the above equations are used.  Whether that is a good idea or not is a discussion for another day. 

The role of the Kalman filter is to produce the best estimate of the state at a given time given the above equations.  To do so, the filter algorithm draws heavily on concepts from Bayesian statistics to produce a maximum likelihood estimate. 

In terms of Bayesian statistics, the algorithm assumes both an a priori state estimate ${\hat x}^{-}_{k}$ and an a posteriori one ${\hat x}_{k}$.  The transition from the a priori to the a posteriori is made with

\[ {\hat x}_k = {\hat x}^{-}_{k} + K_k (z_k – H {\hat x}^{-}_k ) \; , \]

where the ‘magic’ all happens due to the Kalman gain $K_k$ defined as

\[ K_k = P^{-}_k H^T \left( H P^{-}_k H^T + R \right) ^{-1} \; , \]

where ‘$T$’ indicates a matrix transpose.

Note that this equation is functionally similar to the running average form calculated as

\[ {\bar x} = {\bar x}^{-} + \frac{1}{N} \left( x_N – {\bar x}^{-} \right) \; . \]

We’ll return to that similarity in a future post. 

For now, we will round out the menagerie of mathematical beasts by noting that $P_k$ is the state covariance, a $n \times n$, real-valued matrix, that summarizes the current statistical uncertainty in the state estimation.  Formally, it is defined as

\[ P_k = E \left[ (x_k – {\hat x}_k ) (x_k – {\hat x}_k )^T \right] \; , \]

where the ‘$E$’ stands for expectation over the state distribution. 

The state covariance can be associated with the a priori estimate, where it is denoted as $P^{-}_k$ or with the a posteriori estimate, where it is denoted by $P_k$.  The two are related to each other by

\[ P_k = A P^{-}_k A^T + Q \; . \]

The Kalman algorithm is best summarized using the following flow diagram adapted from the one in Introduction to Random Signals and Applies Kalman Filtering 4^th Edition by Brown and Hwang.

In future blogs, we’ll explore how to derive the magical Kalman gain, some applications of it to agent-based time series estimation, and a variety of related topics.  It is worth noting that the notation is fluid, differing from author to author and application to application.

In the last post, we examined the Holt-Winter scheme for tracking the level, trend, and seasonal variations in a time series in a sequential fashion with some synthetic data designed to illustrate the algorithm in as clean a way as possible.  In this post, we’ll try the Holt-Winter method against real world data for US housing sales and will set some of the context for why the method works by comparing it to a related technique called the moving average.

The data analyzed here were obtained from RedFin (https://www.redfin.com/news/data-center/) but it isn’t clear for how long RedFin will continue to make these data public as they list the data as being ‘temporarily released’.  As a result, I’ve linked the data file I’ve used here.

We’re going to approach these data in two ways.  The first is by taking a historical look at the patterns in the data from the vantage point of hindsight on the entire span of home sales having been collected.  In the second approach, we imagine what an agent working in the past thinks as the data come in one record at a time. 

The historical look starts with an overview of the number of homes sold in the time period starting in Feb 2012 and ending at May 2023.

These data show both seasonal and overall trend variations and so our expectation might be that Holt-Winter would do a good job but note two things: First, with the exception of the first pandemic year of 2020, each of the years shows the same pattern: sales are low in the winter months and strong in the summer ones. Second the trend (most easily seen by focusing on the summer peak) shows four distinct regions: a) from 2012-2017 there is an overall upward trend, b) from 2017-2020 the trend in now downward with a much shallower slope, c) the start of the pandemic lockdowns in 2020 breaks the smoothness of the trend and then the trend again has a positive slope over 2020-2021, and d) the trend is strongly downward afterwards.  These data exhibit a real-world richness that the contrived data used in the last post did not and they should prove a solid test for a time series analysis agent/algorithm.

Depending on how ‘intelligent’ we want our analysis agent to be we could look at a variety of other factors to explain or inform these features.  For our purposes, we’ll content ourselves with looking at one other parameter, the median home sales price, mostly to satisfy our human curiosity.

These data look much more orderly in their trend and seasonal variation over the time span from 2012-2020.  Afterwards, there isn’t a clear pattern in terms of trend and season. 

Our final historical analysis will be to try to understand the overall pattern of the data using a moving average defined as:

\[ {\bar x}_{k,n} = \frac{1}{n} \sum_{i =k-n/2}^{k+n/2} x_i \; . \]

The index $k$ specifies to which point of the underlying and $n$ the number of points to be used in the moving average.  Despite the notation, $n$ is best when odd so that there are as many points before the $k$th one as there are after as this prevents the moving average from introducing a bias which shifts a peak in the average off of the place in the data where it occurs.  In addition, there is an art in the selection of the value of $n$ between it being too small, thereby failing to smooth out unwanted fluctuations, and being too large which smears out the desired patterns.  For these data, $n = 5$.  The resulting moving average (in solid black overlaying the original data in the red dashed line) is:

Any agent using this technique would clearly be able to describe the data as having a period of one year with a peak in the middle and perhaps an overall upward trend from 2012 to 2022 but then a sharp decline afterwards.  But two caveats are in order.  First and the most important one, the agent employing this technique to estimate a smoothed value on the $k$th time step must wait until at least $n/2$ additional future points have come in.  This requirement usually precludes being able to perform predictions in real time.  The second is that the moving average is computationally burdensome when $n$ is large.

By contrast, the Holt-Winter method can be used by an agent needing to analyze in real time and it is computationally clean.  At the heart of the Holt-Winter algorithm is the notion of exponential smoothing where the smoothed value at the $k$th step, $s_k$, is determined by the previous smoothed value $s_{k-1}$ and the current raw value $x_k$ according to

\[ s_k = \alpha x_k + (1-\alpha) s_{k-1} \; . \]

Since $s_{k-1}$ was determined from a similar expression at the time point $k-1$, one can back substitute to eliminate all the smoothed values $s$ on the right-hand side in favor of the raw ones $x$ to get

\[ s_k  = \alpha x_k + (1-\alpha)x_{k-1} + (1-\alpha)^2 x_{k-2} + \cdots + (1-\alpha)^k x_0 \; . \]

This expression shows that the smoothed value $s_k$ is a weighted average of all the previous points making it analogous to the sequential averaging discussed in a previous post but the exponential weighting by $(1-\alpha)^n$ makes the resulting sequence $s_k$ look more like the moving average.  In some sense, the exponential smoothing straddles the sequential and moving averages giving the computational convenience of the former while providing the latter’s ability to follow variations and trends.

How closely the exponentially smoothed sequence matches a given $n$-point moving average depends on the selection of the value of $\alpha$.  For example, with $\alpha = 0.2$ the exponentially smoothed curve gives

whereas $\alpha = 0.4$ gives

Of the two of these, the one with $\alpha=0.4$ much more closely matches the 5-point moving average used above. 

The Holt-Winter approach using three separate applications of exponential smoothing, hence the need for the three specified parameters $\alpha$, $\beta$, and $\gamma$.  Leslie Major presents an method for optimizing the selection of these three parameters in her video How to Holts Winters Method in Excel & optimize Alpha, Beta & Gamma. 

We’ll skip this step and simply use some values informed by the best practices that Major (and other YouTubers) note.

The long-term predictions given by our real time agent are pretty good in the time span 2013-2018.  For example, a 24-month prediction made in February 2013 looks like

Likewise, a 24-month prediction in June 2017 looks like

Both have good agreement with a few areas of over or under-estimation.  The most egregious error is the significant overshoot in 2019 which is absent in the 12-month prediction made a year later. 

All told, the real time agent does an excellent job of predicting in the moment but it isn’t perfect as is seen by how the one-month predictions falter when the pandemic hit.

In the last blog, I presented a simple sequential way of analyzing a time series as data are obtained.  In that post, the average of any moment $x^n$ was obtained in real-time by simply tracking the appropriate sums and number of points seen.  Of course, in a real world application, there would have to be a bit more intelligence built into the algorithm to allow an agent employing it to recognize when a datum is corrupted or bad or missing (all real world problems) and to exclude these point both from the running sums and from the number of points processed. 

This month, we look at a more sophisticated algorithm for analyzing trends and patterns in a time series and for projecting that analysis into the future sequential using these patterns.  The algorithm is a favorite in the business community because, once an initial ‘training’ set has been digested, the agent can update trends and patterns with each new datum and then forecast into the future.  The algorithm is called the Holt-Winter triple exponential smoothing and it has been used in the realm of business analytics for forecasting the number of home purchases, the revenue from soft drink sales, ridership on Amtrak, and so on, based on a historical time series of data.

Being totally unfamiliar with this algorithm until recently, I decided to follow and expand upon the fine video by Leslie Major entitled How to Holts Winters Method in Excel & optimize Alpha, Beta & Gamma.  In hindsight, this was a very wise thing to do because there are quite a few subtle choices for initializing the sequential process and the business community focuses predominantly on using the algorithm and not explaining rationale for the choices being followed.

For this first foray, I am using the ‘toy’ data set that Majors constructs for this tutorial.  The data set is clean and well-behaved but, unfortunately, is not available from any link discernable associated with the video but I have reconstructed it (with a lot a pauses) and make it available here. 

The data are sales $W$ of an imaginary item, which, in deference to decades of tradition, I call a widget.  The time period is quarterly and a plot of the definitive sales $W$ from the first quarter of 2003 (January 1, 2003) through the fourth quarter of 2018 (October 1, 2018) shows both seasonal variations (with a monotonic ordering from the first quarter as the lowest to the fourth quarter as the highest)

as well as a definite upward trend for each quarter.

The Holt-Winter algorithm starts by assuming that the first year of data are initially available and that a first guess for a set of three parameters $\alpha$, $\beta$, and $\gamma$ (associated with the level $L$, the trend $T$, and the seasonal $S$ values for the number of widget sales, respectively) are known.  We’ll talk about how to revise these assumptions after the fundamentals of the method are presented.

The algorithm consists of 7 steps.  The prescribed way to initialize the data structures tracking the level, trend, and seasonal values is found in steps 1-4, step 5 is a boot-strap step initialization needed to start the sequential algorithm proper once the first new datum is obtained and steps 6-7 comprise the iterated loop step used for all subsequent data, wherein an update to the current interval is made (step 6) and then a forecast into the future is made (step 7).

In detail these steps require an agent to:

1. Determine the number $P$ of intervals in the period; in this case $P = 4$ since the data are collected quarterly. 
2. Gather the first period of data (here a year) from which the algorithm can ‘learn’ how to statistically characterize it.
3. Calculate the average $A$ of the data in the first period.
4. Calculate the ratio of each interval $i$ in the first period to the average to get the seasonal scalings $S_i = \frac{V_i}{A}$.
5. Once the first new datum $V_i$ ($i=5$) (for the first interval in the second period) comes in, the agent then bootstraps by estimating:
   1. the level in the first interval by making a seasonal adjustment.  Since the seasonal level is not yet known, the agent uses the seasonal value in the previous period in the first interval using $L_i = \frac{V_i}{S_{i-P}}$;
   1. the trend of the first interval in the second period using $T_{i} = \frac{V_i}{S_{i-P}} – \frac{V_{i-1}}{S_{i-1}}$.  This odd looking formula is basically the finite difference between the first interval of the second period and the last interval of the first period, each seasonally adjusted.  Again, since the seasonal level is not yet know, the agent uses the seasonal value from the corresponding earlier interval for the first interval of the second period;
   1. the seasonal ratio of the first interval in the second period using $S_i = \gamma \frac{V_i}{L_i} + (1-\gamma) S_{i-P}$.
6. Now, the agent can begin sequential updating in earnest by using all of the weighted or blended averages of the data in current and past intervals to update:
   1. the level using $L_i = \alpha \frac{V_i}{S_{i-P}} + (1-\alpha)(L_{t-1} + T_{t-1})$
   1. the trend using $T_i = \beta ( L_i – L_{i-1} ) + (1-\beta) T_{t-1}$
   1. the seasonal ratio (again) using $S_i = \gamma \frac{V_i}{L_i} + (1-\gamma) S_{i-P}$
7. Finally, the agent can forecast as far forward as desired (using $F_{i+k} = (L_i + k \cdot T_i) S_{i – P + k}$. where $k$ is an integer representing the number of ‘intervals’ ahead to be forecasted.  There are some subtleties associated with what the agent can do with a finite number of historical levels of the seasonal ratios, so, depending on application, specific approximations for $S_{i – P + k}$ must be made.

Using the widget sales data, the first 4-quarter forecast compares favorable to the actuals as seen in the following plot.

When forecasting only a quarter ahead, as Major herself does, the results are also qualitatively quite good.

Finally, a note about selecting the values of $\alpha$, $\beta$, and $\gamma$.  There is a general rule of thumb for initial guesses but that the way to nail down the best values is to use an optimizer to minimize the RMS error between a forecast and the actuals.  Majors discusses all of these points and shows how Excel can be used in her video to get even better agreement.

For next month, we’ll talk about the roots of the Holt-Winter algorithm in the exponential smoother (since it is applied to three parameters – level, trend, and seasonal ratio – that is why the algorithm is often called triple exponential smoothing).

A hallmark of intelligence is the ability to anticipate and plan as events occur as time elapses.  Evaluating and judging each event sequentially is how each of us lives but, perhaps ironically, this is not how most of us are trained to evaluate a time series of data.  Typically, we collect quantitative and/or qualitative data for some time span, time tagging the value of each event, and then we analyze the entire data set in as one large batch.  This technique works well for careful, albeit leisurely, exploration of the world around us.

Having an intelligent agent (organic or artificial) working in the world at large necessitates using both techniques – real time evaluation in some circumstances and batch evaluation in others – along with the ability to distinguish when to use one versus the other.

Given the ubiquity of time series in our day-to-day interactions with the world (seasonal temperatures, stock market motion, radio and TV signals) it seems worthwhile to spend some space investigating a variety of techniques for analyzing these data.

As a warmup exercise that demonstrates the differences between real time and batch nuances involved, consider random numbers pulled from a normal distribution with a mean ($\mu = 11$) and standard deviation ($\sigma = 1.5$). 

Suppose that we pull $N=1000$ samples from this distribution.  We would expect that the sample mean, ${\bar x}$, and sample deviation $S_x$ to be equal to the population mean and standard deviation to within 3% (given that $1/\sqrt(1000) \approx 0.03$).  Using numpy, we can put that expectation to the test, finding that for one particular set of realizations that the batch estimation over the entire 1000-sample set is ${\bar x} = 11.08$ and $S_x = 1.505$.

But how would we estimate the sample mean and standard deviation as points come in?  With the first point, we would be forced to conclude that ${\bar x} = x_0$ and $S_x = 0$.  For subsequent points, we don’t need to hold onto the values of the individual measurements (unless we want to).  We can develop an iterative computation starting with the definition of an average

\[ {\bar x} = \frac{1}{N} \sum_{i=1}^N x_i \; .\]

Separating out the most recent point $x_N$ and multiplying the sum over the first $N-1$ points by the $1 = (N-1)/(N-1)$ gives

\[ {\bar x} = \frac{N-1}{N-1} \frac{1}{N} \left( \sum_{i=1}^{N-1} x_i \right) + \frac{1}{N} x_N \; .\]

Recognizing that the first term contains the average ${\bar x}^{(-)}$ over the first $N-1$ points, this expression can be rewritten as

\[ {\bar x} = \frac{N-1}{N} {\bar x}^{(-)} + \frac{1}{N} x_N \; .\]

Some authors then expand the first term and collect factors proportional to $1/N$ to get

\[ {\bar x} = {\bar x}^{(-)} + \frac{1}{N} \left( x_N – {\bar x}^{(-)} \right) \; .\]

Either of these iterative forms can be used to keep a running tally of the mean.  But since the number of points in the estimation successively increases as a function of time, we should expect that difference between the running average and the final batch estimation to also be a function of time.

While there is definitive theory that tells us the difference between the running tally and the population mean there isn’t any theory that characterizes how it should rank relative to the batch estimation other than the generic expectation that as the number of points used in the running tally approaches the number in the batch estimation that the two should converge.  Of course, the final value must exactly agree as there were no approximations made in the algebraic manipulations above.

To characterize the performance of the running tally, we look at a variety of experiments.

In the first experiment, the running tally fluctuates about the batch mean before settling in and falling effectively on top.

But in the second experiment, the running tally starts far from the batch mean and (with only the exception of the first point) stays above the until quite late in the evolution.

Looking at the distribution of the samples on the left-hand plot shows that there was an overall bias relative to the batch mean with a downward trend, illustrating how tricky real data can be.

One additional note, the same scheme can be used to keep a running tally on the average of $x^2$ allowing for a real time update of the standard deviation from the relation $\sigma^2 = {\bar {x^2}} – {\bar x}^2$.

As the second case demonstrates, our real time agent may have a significantly different understanding of the statistics than the agent who can wait and reflect over a whole run of samples (although there is a philosophical point as to what ‘whole run’ means).  In the months to come we’ll explore some of the techniques in both batch and sequential processing.