Collatz Conjecture

Big things come in small packages.  From tiny acorns grow mighty oaks.  Never judge a book by its cover.  These familiar euphemisms try to capture, in a pithy way, the basic idea that simple looking systems can often hide a surprising amount of complexity.   This basic observations couldn’t more true than in the case of the Collatz Conjecture.

The Collatz Conjecture is so simple that, on the face of it, it must be easy to prove.  But like other easily stated suppositions in mathematics, the proof, if one exists, must be particularly difficult to construct, since it has eluded mathematicians for nearly 100 years.

In a nutshell, the Collatz Conjecture says that a particular process, described just below, when repeatedly applied to any integer always ends up the same way, regardless of the starting value of the integer.  The process, referred to as the Half or Triple-Plus-One (HTPO) process, is as follows:

There it is.  It is so simple that it can be implemented in a few lines in just about any language; probably even in COBOL.  And yet, proving that this conjecture is actually so hard that the famous mathematician Paul Erdös is credited with saying

Obviously this column is not going to present a proof but it is going to explore some of the properties of the conjecture – including a few that may not have been seen in the literature.  There are two reasons for doing so.

The first reason is the sheer joy and delight that arises from seeing inexplicable complexity arise out of such simple rules.  Amazingly rich plots results simply by looking at the data from numerical experiments in a variety of different ways.  What, at first, may look like randomness resolves itself in patterns later on as the number of integers examined is increased.

The second reason is less about mathematics and far more about human reason.  Why a proof is hard to find is a topic in epistemology worth exploring all on its own.  Consider that the Collatz conjecture is a system that is far easier to encode in a computer than say the solution to an orbital mechanics problem or the motion of a fluid over a fixed object like an airplane wing.  No calculus or linear algebra is required.  Nowhere does one need real or complex numbers.  All the machinery that is needed is learned in elementary school and yet the proof is much harder than those associated with the ‘more advanced’ topics.  Surely there is a Socratic lesson buried in all of this. But before we explore that topic, let’s look at the Collatz conjecture in detail.

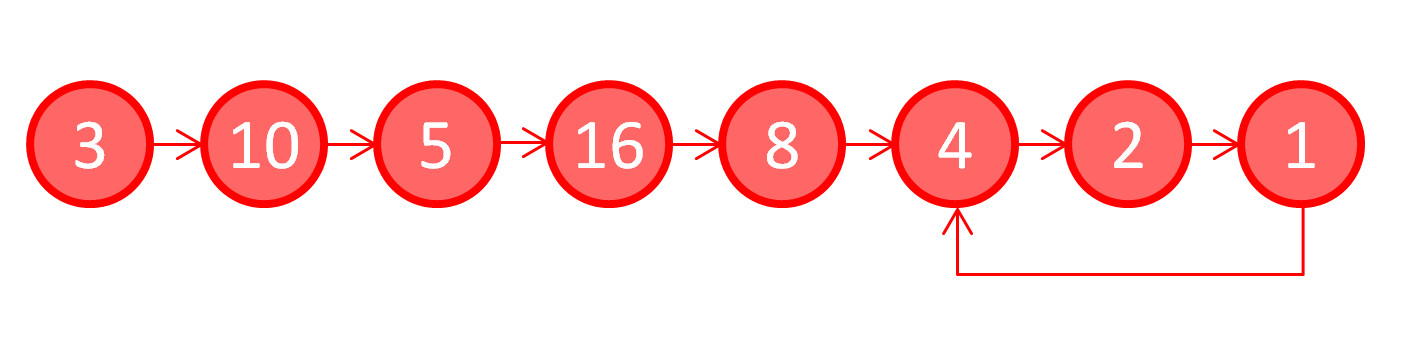
Pick an integer, say $n = 3$, and apply the HTPO process to it.  Since 3 is odd, the resulting value is 10.  Now use 10 and the next value and again apply the HTPO process.  Since 10 is even, the resulting value is 5.  Starting from here and applying in succession leads to the following ‘trajectory’.

Note how the sequence of numbers rises and falls getting up as high as 16 and falling as low as 1.  This is called a hailstone sequence since it is reminiscent of the multiple rises and falls of a hailstone during a thunderstorm.  Also note that once the number 1 is reached the sequence is now trapped in the infinitely-repeating ‘4-2-1’ loop.  It is customary to stop the iterations when 1 is reached for the first time and to declare that the sequence has stopped.  By convention, the number of integers in the sequence (including the starting value) is declared as the stopping time.  Thus the stopping time for a starting value of 3 is 8, the number of unique circles in the figure.

The Collatz Conjecture is then the statement that the number 1 is always reached no matter what the initial value may be.  While the proof of this assertion has not be obtained, huge numbers have been tested (2⁶⁰ = 1,152,921,504,606,846,976 ) and none have failed to reach 1 and settle into the ‘4-2-1’ loop.

Investigators, looking for a proof, have employed a number of tools in an attempt to better understand what makes this conjecture so shy in being characterized with a logical proof.  Many of these tools are visualizations of the stopping times as a function of initial value.

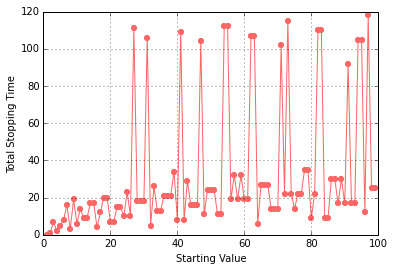
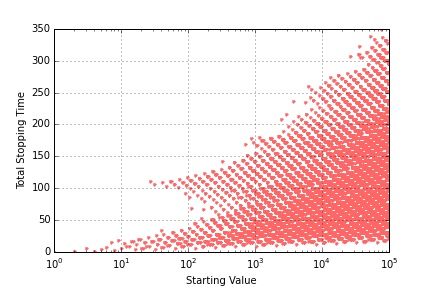
The following figure is one such plot showing the stopping times for the first 100 integers.

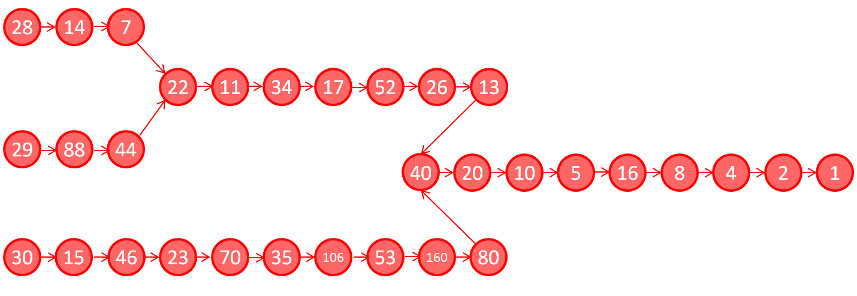
It is remarkable that there is no smooth pattern in the results.  Adjacent integers, such as 26 and 27, can have wildly different stopping lengths, 10 versus 111, respectively, while adjacent pairs can have identical stopping lengths.  Particularly noteworthy is the fact that the integers 28, 29, and 30 all have a stopping length of 18 despite their rather different trajectories:

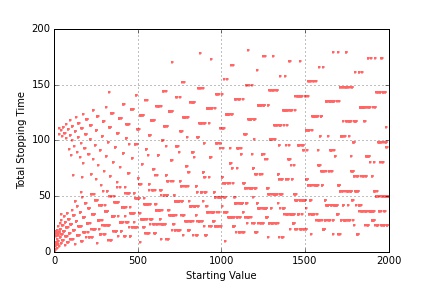
The jerky or random character of the stopping length plot for the first 100 integers transitions into something more akin to patterns within patterns when the number of integers surveyed increases to 2000.

There seem to be overlapping curves asymptotically rising and falling, layered one on top of the other with large regions where they interleave.

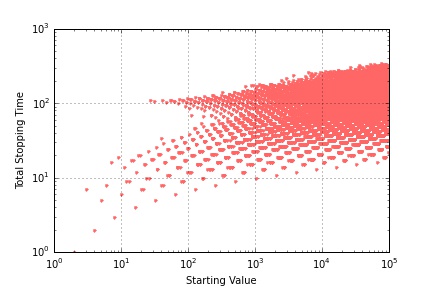
Different visualizations reveal different structures.  For example, the stopping times for the first 10000 integers, plotted on a semilog plot

reveal a general triangular shape, whereas the same data shown on a full log-log plot shows

that the values are tending to cluster rather that moving in a unbounded fashion.

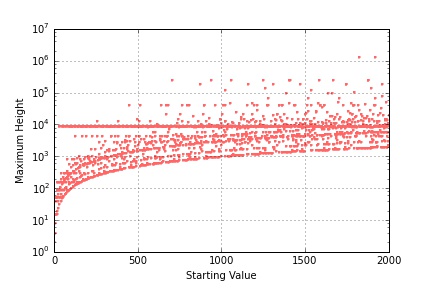
This latter observation opened another line of inquiry centered on just how high does the hailstone trajectory go rather than how long does it take for it to land.  A little bit of additional coding to capture the full trajectory for the first 2000 integers reveals that one value, 9232, tends to be hit more often than all the others.

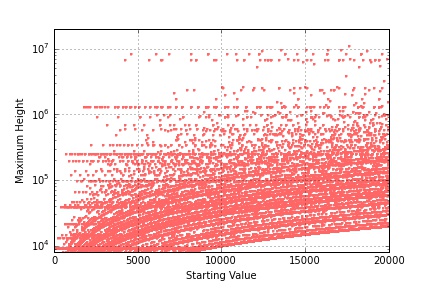
There is a strong line visible just under 10⁴ on the plot and some simple statistics show that 9232 forms 16% of all the highest values in the first 100 integers and about 33.8% for the first 2000.  As the integer range increases to 20000, additional horizontal attractors (to coin a term in relation to the Collatz Conjecture) come in, although it is difficult to pick out just how prominent they are due to the business of the plot.

It is interesting to see just how low these horizontal attractors extend.

As this column closes, it is worth repeating that all of this structure comes from a repeated application of the HTPO process for a finite number of times.  The fact that mathematics can’t say whether the process will stop for arbitrary integers is astonishing and speaks to many of the basic complexities that arise in proof and logic when the repeated operations are involved.  It seems that if Socrates were alive and playing with the Collatz Conjecture he might be inclined to point out that the only wisdom is knowing that we don’t know very much.