A central concept of Socratic and Platonic thought is the idea of an ideal form. It sits at the base of all discussions about knowledge and epistemology. Any rectangle that we draw on paper or in a drawing software package, that we construct using rulers and scissors, or manufacture with computer controlled fabrication is a shadow or reflection of the ideal rectangle. This ideal rectangle exists in the space of forms, which may be entirely within the human capacity to understand the world and distinguish or may actually have an independent existence outside the human mind, reflecting a high power. All of these notions about the ideal forms are familiar from the philosophy from antiquity.
What isn’t so clear is what Plato’s reaction would be if he were suddenly transported forward in time and plunked down in a classroom discussion about the propagation of error. The intriguing question is would he modify his philosophical thought to expand the concept of an ideal form to include and ideal form of error?
Let’s see if I can make this question concrete by the use of an example. Consider a diagram representing an ideal rectangle of length $L$ and height $H$.
Euclidean geometry tells us that the area of such a rectangle is given by the product
\[ A = L \cdot H \; . \]
Of course, the rectangle represented in the diagram doesn’t really exist since there are always imperfections and physical limitations. The usual strategy is to not take the world as we would like it to be but to take it as it is and cope with these departures from the ideal.
The departures from the ideal can be classified into two broad categories.
The first category, called knowledge error, contains all of the errors in our ability to know. For example, we do not know exactly what numerical value to give the length $L$. There are fundamental limitations on our ability to measure or represent the numerical value of $L$ and so we know the ‘true’ value of $L$ only to within some fuzzy approximation.
The second category doesn’t seem to have a universally agreed-upon name, reflecting the fact that, as a society, we are still coming to grips with the implications of this idea. This departure from the ideal describes the fact that at some level there may not even be on definable concept of true. Essentially, the idea of the length of an object is context-dependent and may have no absolutely clear idea at the atomic level due to the inherent uncertainty in quantum mechanics. This type of ‘error’ is sometimes called aleatory error (in contrast to epistemic error; synonymous with knowledge error).
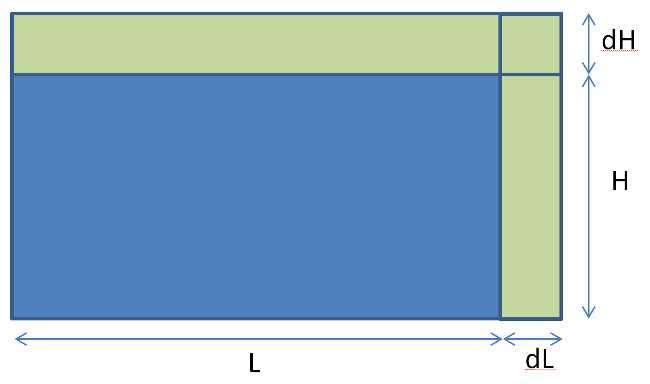
Taken together, the knowledge and aleatory errors contribute to an uncertainty in length of the rectangle of $dL$ and an uncertainty in its height of $dH$.
Scientists and engineers are commonly exposed to a model in determining the error in the area of such a rectangle as part of their training to deal with uncertainty and error in a formula sometimes called the propagation of error (or uncertainty). For the case of this error-bound rectangle, the true area, $A’$, is determined also in Euclidean fashion yielding
\[ A’ = (L+dL) \cdot (H+dH) = L \cdot H + dL \cdot H + L \cdot dH + dL \cdot dH .\]
So the error in the error in the area, denoted as $dA$, has a more complicated form that the area itself
\[ dA = dL \cdot H + L \cdot dH + dL \cdot dH \; . \]
Now suppose that Plato were in the classroom when this lesson was taught. What would his reaction be? I bring this up because although the treatment above is meant to handle error it is still an idealization. There is still a notion of an ideal rectangle sitting underneath.
The curious question that follows in its train is this: is there an ideal form for this error idealization? In other words, is there a perfect or ideal error in the space of forms of which our particular error discussion is a shadow or reflection?
It may sound like this question if predicated on a contradiction but my contention is that it only seems so, on the surface. In understanding the propagation of error in the calculation of the rectangle I’ve had to assume a particular functional relationship.
It is a profound assumption that the object drawn above (not what it represents but that object itself), which is called a rectangle but which is embodied in the real world as made up of atomic parts (be they physical atoms or pixels), can be characterized by two numbers ($L$ and $H$) even if I don’t know what values $L$ and $H$ take on. In some sense, this idealization should sit in the space of forms.
But if that is true, what stops us there. Suppose we had a more complex functional relationship, something, say, that tries to model the boundaries of the object as a set of curves that deviate much from linearity but enough to capture a shaky hand when the object was drawn or a manufacturing process with deviations when machined. Is this model not also an idealization and therefore a reflection of something within the space of forms?
And why stop there. It seems to me that the boundary line between what is and is not in the space of forms is arbitrary (and perhaps self-referential – is the boundary between what is and is not in the space of forms itself in the space of forms). Like levels of abstraction in a computer model depend on the context, could not the space of forms depend on the questions that are being asked.
Perhaps the space of forms is as infinite or as finite as we need it to be. Perhaps its forms all the way down.